Лекция 6. Понятие полноты множества функций. Замкнутые классы
Интерес к разложению булевых функций в канонический полином Жегалкина объясняется прежде всего тем, что такое представление реализуемых функций является основой для синтеза логических схем в базисе элементов И и СЛОЖЕНИЕ по МОДУЛЮ ДВА.
Определение. Полином булевой функции F, в слагаемые которого все переменные F входят только без отрицания или только с отрицанием, называется монотонно-поляризованным. Причем в первом случае полином функции F называется положительно-поляризованный и обозначается через P(F), а во втором случае - отрицательно-поляризованным и обозначается через Q(F). Полином P(F) иначе называется каноническим полиномом Жегалкина (или в зарубежной научно-технической литературе - формой Рида-Мюллера). Например, для булевой функции, заданной вектором значений таблицы истинности w(F)=(00100111) полиномы P(F) и Q(F) имеют вид:
Отметим некоторые свойства монотонно-поляризованных полиномов P(F) и Q(F) булевой функции 1. Полиномы P(F) и Q(F) являются для булевой функции F единственными. 2. Полиномы P(F) и Q(F) имеют степень n тогда и только тогда, когда таблица истинности функции F содержит нечетное число единиц. 3. Число слагаемых полинома P(F) (Q(F)) четно тогда и только тогда, когда
Основным достоинством представления булевых функций в виде канонического полинома Жегалкина является то, что в этом представлении любая булева функция задается с помощью всего двух логических операций: конъюнкции и сложения по модулю два, что сокращает набор различных элементов для синтеза логических схем. Опишем метод построения канонического полинома Жегалкина P(F) путем преобразования СДНФ для произвольных булевых функций n переменных F, заданных посредством таблицы истинности. Предварительно отметим основные свойства логической операции сложения по модулю два, которые используются при описании метода.Имеет место
если Метод построения полинома P(F) заключается в последовательном выполнении следующих действий: 1) выписывается СДНФ булевой функции F; 2) на основе применения (6) СДНФ F преобразуется в СПНФ функции F; 3) в СПНФ все переменные с отрицанием заменяются по формуле (2); 4) в скобочной форме осуществляется раскрытие скобок согласно (3); 5) из полученного выражения удаляются попарно одинаковые слагаемые в соответствии с (1); 6) полученное выражение обозначается через P(F). Пример. Составить канонический полином Жегалкина P(F) булевой функции, если СДНФ данной булевой функции, имеет вид: Решение. Заменим операцию дизъюнкции операцией сложения по модулю два по (6). При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю. Следовательно, СПНФ будет иметь вид:
Все переменные с отрицанием заменяем по формуле (2), затем раскрываем скобки и из полученного выражения удаляем попарно одинаковые слагаемые в соответствии с (1):
Ответ: P(F) Определение. Система функций Из теоремы 8.2 следует, что система Теорема. Если все функции функционально полной системы Пример. а) Системы
С точки зрения функциональной полноты систему б) Системы
Таким образом, система в) Система На свойствах этой системы остановимся подробнее. Определение. Множество Всякая система Пример. а) Множество всех дизъюнкций, то есть функций вида б) Множество всех линейных функций является замкнутым классом, так как подстановка формул вида Важнейшим примером замкнутого класса является класс монотонных функций, который будет рассмотрен далее. Ранее рассматривалось отношение частичного порядка Определение. Функция Пример. а) Функция б) Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями. в) Рассмотрим две функции от трёх переменных, заданных следующей таблицей.
Функция Проверка монотонности функции непосредственно по определению требует анализа таблицы функции и может оказаться достаточно трудоёмкой. Поэтому весьма полезной для установления монотонности является следующая теорема. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний. Теорема. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний. Из данной теоремы и того очевидного факта, что подстановка нескольких формул без отрицаний в формулу без отрицаний снова даёт формулу без отрицаний, вытекает следующая теорема. Теорема. Множество всех монотонных функций является замкнутым классом. Но поскольку всякая булева формула без отрицаний является суперпозицией дизъюнкций и конъюнкций, из данной теоремы непосредственно получаем следствие. Следствие. Класс монотонных функций является замыканием системы функций
|

 ,
, .
.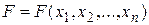 :
: (соответственно
(соответственно  ).
). (1)
(1) (2)
(2) (3)
(3) (4)
(4) , если
, если  (5)
(5) , (6)
, (6) для
для  ,
,  ,
,  .
. .
. .
.

 .
. называется функционально полной системой, если любая логическая функция может быть представлена формулой над системой
называется функционально полной системой, если любая логическая функция может быть представлена формулой над системой  является функционально полной. Равным образом, функционально полна любая система
является функционально полной. Равным образом, функционально полна любая система  из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы
из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы  представимы формулами над системой
представимы формулами над системой  и
и  функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до
функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до  через остальные две:
через остальные две: .
. и
и  не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания.
не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания. (штрих Шеффера) и
(штрих Шеффера) и 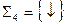 (стрелка Пирса) являются функционально полными.
(стрелка Пирса) являются функционально полными. .
. сводится к системе
сводится к системе  - к системе
- к системе  (
( умножение по модулю 2,
умножение по модулю 2,  сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку
сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку  , данная система сводится к
, данная система сводится к  логических функций называется замкнутым классом, если любая суперпозиция функций из множества
логических функций называется замкнутым классом, если любая суперпозиция функций из множества 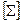 . Если множество
. Если множество  .
. является замкнутым классом.
является замкнутым классом. после преобразований даёт формулу такого же вида.
после преобразований даёт формулу такого же вида. на множестве векторов одинаковой длины. Напомним, что для векторов
на множестве векторов одинаковой длины. Напомним, что для векторов  и
и  выполняется
выполняется  , если для любого
, если для любого  выполняется
выполняется  . Здесь воспользуемся этим отношением для двоичных векторов.
. Здесь воспользуемся этим отношением для двоичных векторов. называется монотонной, если для любых двух двоичных наборов длины
называется монотонной, если для любых двух двоичных наборов длины  из того, что
из того, что 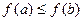 .
. монотонна.
монотонна.




 , а
, а  . Монотонность функции
. Монотонность функции 


