Элементарные булевы функции. Равносильности
Булевых (или логических) функций от одной переменной
Основные элементарные булевы функции от двух переменных приведены в следующей таблице:
Функция Функция Кроме таблицы истинности, булевы функции могут быть заданы аналитически с помощью формул. Например, Если формула a реализует булеву функцию F, которая тождественно равна единице, то она называется тождественно истинной. Если формула a реализует булеву функцию F, которая тождественно равна нулю, то она называется тождественно ложной. Если формулы a и b зависят от одних и тех же переменных и реализуют одну и ту же булеву функцию F, то формулы a и b называются равносильными.
|

 . Они приведены в следующей таблице:
. Они приведены в следующей таблице:
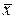
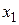




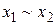



 , но чаще всего знак конъюнкции аналогично знаку умножения опускают и пишут
, но чаще всего знак конъюнкции аналогично знаку умножения опускают и пишут  . Конъюнкция
. Конъюнкция  .
.


