Формулы логики высказываний
Основная задача логики высказываний состоит в изучении логических форм составных высказываний с помощью логических операций. Понятие логической формы составного высказывания уточняется с помощью вводимого понятия формулы логики высказываний. Понятие формул логики высказываний определяется следующим образом: 1. Элементарные формулы – атомы – являются формулами логики высказываний. 2. Если A, B – формулы, то 3. только те выражения являются формулами логики высказываний, для которых это следует из 1, 2. Согласно определения, всякая формула либо атом, либо образуется из атомов в результате применения 2. Число скобок в формулах можно уменьшить, если опустить внешнюю пару скобок и упорядочить знаки логических операций по старшинству: «, →, Знак «имеет самую большую область действия, знак Определение. Формулы логики, принимающие значение " истина" при любых значениях атомов, входящих в формулу, называется тождественно истинными (или законами логики, или тавтологиями). Например, формула Определение. Формулы логики, принимающие всегда ложное значение, называются тождественно ложными (или противоречиями). Например, формула Определение. Формулы алгебры логики, принимающие значение «ложь» хотя бы на одном наборе значений атомов, входящих в формулу называются опровержимыми. Определение. Формулы алгебры логики, принимающие значение «истина» хотя бы на одном наборе значений атомов, входящих в формулу называются выполнимыми. Определение. Формулы Р и Q называются равносильными, если их истинностные значения совпадают при любом выборе истинностных значений атомов, входящих в эти формулы. Запись Р
Лекция 3. Изучение законов логики. Равносильные преобразования.
|

 , (A
, (A  B), (A
B), (A  B), (A→ B), (A«В) также являются формулами логики высказываний.
B), (A→ B), (A«В) также являются формулами логики высказываний. .
.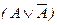 всегда тождественно истинна.
всегда тождественно истинна. - противоречие.
- противоречие. Q означает, что формулы Р и Q равносильны.
Q означает, что формулы Р и Q равносильны.


