Лекция 4. Булевы функции
Переменная х, принимающая значения 0 или 1, называется булевой (или логической, двоичной). Функция F, зависящая от булевых переменных Булевы функции F от n переменных В качестве примера рассмотрим таблицу истинности некоторой булевой функции F, зависящей от переменных
Булева функция n переменных F однозначно определяется Рассматриваемая булева функция F принимает значения 0 на наборах 000, 001, 011 и 100, а значение 1 - на наборах 010, 101, 110 и 111. Множество наборов, на которых функция F принимает значение 1, называется характеристическим и обозначается через N F. В настоящем примере имеет место N F = (010, 101, 110, 111). Общее число различных булевых функций F от n переменных равно
|
и принимающая также значения 0 или 1, называется булевой (или логической, двоичной) и обозначается 
.
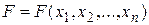могут быть заданы посредством таблицы истинности, содержащей 
строк и 
столбцов. В левой части таблицы содержатся наборы значений n переменных, расположенные в порядке возрастания их десятичного эквивалента, а в правой ее части - значения функции F на соответствующих наборах значений переменных.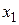
, 
и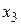 
.
- разрядным булевым вектором ее значений w(F) (т.е. w(F) - таблица истинности функции F). Например, в этом примере имеем w(F)=(00100111).
. Т.е. число булевых функций от двух переменных равно 
, от трех переменных 
.
