Дополнительные равносильности
Переменная Пример. С помощью основных равносильностей доказать, что в булевой функции F = Решение. Применяя закон поглощения и закон склеивания, получим F = Так как существует такая формула, реализующая эту булеву функцию, в которой отсутствует Пример. С помощью таблицы истинности убедиться в справедливости законов де Моргана Решение. Построим таблицу истинности для
Так как в таблице истинности булевым функциям Пример. С помощью основных равносильностей доказать закон обобщенного склеивания Решение. Применяя закон склеивания (в обратном порядке, то есть
Пример. С помощью основных равносильностей доказать, что Решение. Применяя основные равносильности, получим
|
,
,
,
,
,
,
,
,
, 
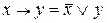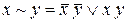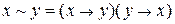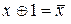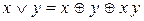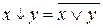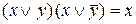(законы склеивания),
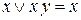(закон поглощения).
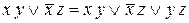(закон обобщенного склеивания).
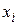булевой функции F называется несущественной (или фиктивной), если 
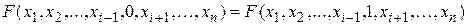, то есть если изменение значения 
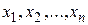не меняет значения функции. При этом существует такая формула, реализующая эту булеву функцию, в которой отсутствует 
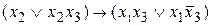переменная 
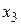является фиктивной.
.
.
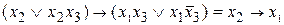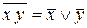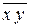и 
.
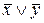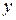
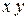
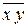
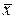
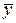
) и 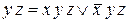дистрибутивность (то есть вынесем за скобки 
), получим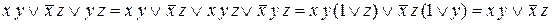
.
.
.
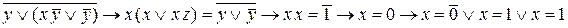