Конъюнктивные нормальные формы
Определение. Элементарной дизъюнкцией называется дизъюнкция литералов (переменных или их отрицаний), взятых не более чем по одному разу. Например, дизъюнкции Следующие дизъюнкции: Определение. Элементарная дизъюнкция булевой функции Определение. Конъюнкция любого конечного множества элементарных дизъюнкций булевой функции F называется конъюнктивной нормальной формой (КНФ) функции F. Число элементарных дизъюнкций, составляющих КНФ, называется длиной КНФ. Например, КНФ Для произвольной булевой функции F существует, вообще говоря, много различных реализующих ее КНФ, отличающихся друг от друга длиной, числом вхождений литералов и т.д. Определение. Две (или несколько) КНФ, реализующих одну и ту же булеву функцию F, называются эквивалентными (или равносильными). Определение. КНФ булевой функции F, состоящая только из полных элементарных дизъюнкций, называется совершеннойКНФ(СКНФ). Например, Отметим, что КДНФ является единственной (с точностью перестановки множителей) для конкретной булевой функции F.
Любую булеву функцию F, заданную формулой, можно с помощью основных равносильностей преобразовать к КНФ, а затем к СКНФ. Пример. Привести к виду СКНФ булеву функцию F = Решение. С помощью основных равносильностей преобразуем к КНФ:
В данном примере сначала выразили функцию только с помощью операций дизъюнкции, конъюнкции и отрицания, а затем несколько раз применили формулу Применяя закон склеивания (в обратном порядке:
Так как Составим таблицу истинности для булевой функции F = Таблица истинности СКНФ
В общем случае также можно вывести закономерности построения СКНФ по таблице истинности булевой функции, что является очень удобным. СКНФ состоит из конъюнкций полных элементарных дизъюнкций наборов переменных Пример. По таблице истинности составить СКНФ.
Решение: F Пример. Для булевой функции, заданной в виде ДНФ Решение: Применяя формулу
Применяя закон склеивания (в обратном порядке:
Так как
Таблица истинности СКНФ
|

 ,
,  , 1 являются элементарными. Причем первая элементарная дизъюнкция имеет ранг (число литералов) 2, вторая - 3, а третья - 0.
, 1 являются элементарными. Причем первая элементарная дизъюнкция имеет ранг (число литералов) 2, вторая - 3, а третья - 0. ,
,  ,
,  ,
, 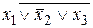 , 0 не являются элементарными.
, 0 не являются элементарными.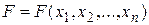 , содержащая n литералов, называется полной.
, содержащая n литералов, называется полной.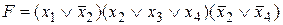 имеет длину, равную 3.
имеет длину, равную 3. - СКНФ функции F, заданной вектором значений таблицы истинности w(F)=(01100111).
- СКНФ функции F, заданной вектором значений таблицы истинности w(F)=(01100111).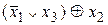 .
.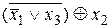 =
=  =
= 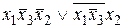 =
= =
= 
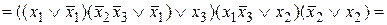



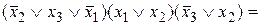
 ― КНФ.
― КНФ. , группируя переменные таким образом, чтобы каждый раз одна скобка в конъюнкции сокращалась по формуле
, группируя переменные таким образом, чтобы каждый раз одна скобка в конъюнкции сокращалась по формуле  .
. ), дополняем дизъюнкции
), дополняем дизъюнкции  ,
,  до полных элементарных дизъюнкций:
до полных элементарных дизъюнкций: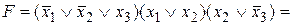
 .
. , то после сокращения одинаковых конъюнкций получаем СКНФ: F
, то после сокращения одинаковых конъюнкций получаем СКНФ: F 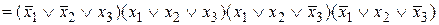 .
.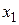

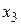







 , на которых функция принимает значение 0. Переменные берутся без отрицания, если им соответствует в таблице истинности 0, с отрицанием, если 1.
, на которых функция принимает значение 0. Переменные берутся без отрицания, если им соответствует в таблице истинности 0, с отрицанием, если 1. .
.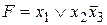 , составить КНФ, СКНФ и выполнить проверку по таблице истинности.
, составить КНФ, СКНФ и выполнить проверку по таблице истинности.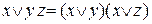 , из ДНФ получаем КНФ:
, из ДНФ получаем КНФ: .
.
 .
.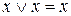 , то после сокращения одинаковых дизъюнкций получаем СКНФ:
, то после сокращения одинаковых дизъюнкций получаем СКНФ: .
.