Логические операции
Пусть A, В - произвольные высказывания, относительно которых не предполагается, что известно их истинностные значения. Связке " НЕ" соответствует логическая операция отрицания, обозначение операции – знак ù или Определение. Отрицанием высказывания A называется высказывание Таблица истинности отрицания:
Пример: A: 2*2=4 – истинное высказывание; Связке " И" соответствует операция конъюнкция, обозначение операции – знак Определение. Конъюнкцией высказываний A и B называется высказывание A Таблица истинности конъюнкции:
Пример: A: 5 – нечетное число; B: Пушкин родился в 1799 г – истинные высказывания; поэтому высказываниеA Связке " ИЛИ" соответствует операция дизъюнкция, обозначение операции – знак В формально-логических выводах «или» употребляется не в исключающем смысле (в отличие от обыденной речи, где эта связка может употребляться и в исключающем смысле и в неисключающем смысле) Определение. Дизъюнкцией высказываний A и B называется высказывание A Таблица истинности дизъюнкции:
Пример. A: 7< 10, и.в. В: 3 - число четное, л.в. A Связке " ЕСЛИ....ТО" соответствует логическая операция импликация, обозначение операции знак →. Определение. Импликацией высказываний A и B называется высказывание A→ B (читается " если A, то B"), которое ложно тогда и только тогда, когда A – истинно, а B – ложно. Таблица истинности импликации:
Пример. A: 2*2=5, л. в. В: 2=2, и. в. A→ B: 2*2=5→ 2=2. и. в. Высказывание A называется условием или посылкой, высказывание В - заключением или следствием импликации. Связке " ТОГДА И ТОЛЬКО ТОГДА, КОГДА" соответствует операция эквиваленция, обозначение операция – знак «. Определение. Эквиваленцией высказываний A и В навивается высказывание, обозначаемое A«B (читается: " A тогда и только тогда, когда В" или короче: " A эквивалентно В"), которое считается истинным только тогда, когда оба высказывания A и В имеют одинаковое истинностное значение. Эквивалентность А«В читается также следующим образом: " Для того, чтобы A, необходимо и достаточно, чтобы В". Таблица истинности эквиваленции:
Пример. A: 7 – число простое; и.в. В: в равнобедренном треугольнике при основании углы равны, и.в. A«В - и.в. 1) Стрелка Пирса - ↓. Логическая операция задается таблицей:
Стрелка Пирса является отрицанием дизъюнкции. 2) Штрих Шеффера - |. Логическая операция задается таблицей:
Штрих Шеффера является отрицанием конъюнкции. 3) Сумма по модулю два - Логическая операция задается таблицей:
Сумма по модулю два является отрицанием эквивалентности
|

 .
. (ù A), которое истинно, если A – ложно, и ложно, если A – истинно.
(ù A), которое истинно, если A – ложно, и ложно, если A – истинно.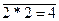 или 2*2
или 2*2  4 - ложное высказывание.
4 - ложное высказывание. (или &).
(или &). .
.



