Сочетания с повторениямиПример. На почте имеются открытки четырех видов: красные, желтые, зеленые и синие. Требуется 10 открыток. Сколькими способами можно их скомбинировать? Решение: Пусть мы отобрали 4 красных, 2 желтых, 2 зеленых и 2 синих открытки. Составим кортеж из 0 и 1. Выпишем столько единиц, сколько красная открытка встречается в нашем наборе, и поставим 0: 11110. Затем добавим кортеж для желтых -110. Получим 11110110. Добавим кортеж для зеленых и синих открыток. В последнем 0 не ставим. Получим кортеж 1111011011011. В нем 10 единиц и 3 нуля. Общая длина кортежа – 13. Таких кортежей можно составить столько, сколько перестановок с повторениями из 13.
В общем случае. Пусть мы имеем n элементов Единиц – k. Нулей – n-1. Длина кортежа n+ k -1 Общее число сочетаний с повторениями Ĉ
Итак, Ĉ
|
(10, 3)= 
= 286 – это и будет число сочетаний с повторениями из 4 по 10.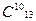
Таким образом, Ĉ 
, 
, из которых создаются сочетания с повторениями, и каждое сочетание содержит k элементов. Составим кортеж, который запишем вначале столько единиц, сколько элемент 
и т.д. без последнего нуля. Получим: 111…1011…10…11…1
= 
(k, n-(k -1))= 
= 
,
