1. Для спрощення арифметичних операцій числа в цифрових пристроях подаються спеціальними кодами - прямим, оберненим і додатковим.
Прямий код двійкового числа містить цифрові розряди, ліворуч від яких записується знаковий розряд. Додавання в прямому коді чисел, що мають однакові знаки, виконуються досить просто. Цифрові розряди чисел складаються за правилами арифметики і сумі привласнюється код знака доданків. Значно складніше реалізується в прямому коді операція алгебричного віднімання, тобто додавання чисел, що мають різні знаки У цьому разі доводиться визначати більше за модулем число, вираховувати числа і привласнювати різниці знак більшого за модулем числа.
2. За допомогою оберненого і додаткового кодів операція віднімання (чи алгебричного додавання) зводиться до арифметичного додавання, спрощується визначення знака результату операції, а також полегшується вироблення ознак переповнення результату (коли в результаті арифметичних операцій число стає більшим від максимально допустимого для цієї форми значення).
Обернений код від'ємного числа одержується за таким правилом: у знаковий розряд числа записується одиниця, у цифрових розрядах ну замінюються одиницями, а одиниці - нулями.
3. Додатковий код від'ємного числа отримують з оберненого коду додаванням одиниці до молодшого розряду.
Подання від'ємного числа -10910 у прямому коді та його перетворення в обернені і додатковий коди показано на рис.
Під час виконання операції алгебричного додавання з використанням оберненого чи додаткового коду додатні числа подаються прямим кодом, а від'ємні - оберненим чи додатковим кодом. Потім виконується арифметичне підсумовування цих кодів, включаючи знакові розряди, що при цьому розглядаються як старші. У разі використай оберненого коду виникла одиниця перенесення зі знакового розряду циклічно додається до молодшого розряду суми кодів, а у разі використання додаткового коду ця одиниця вилучається.
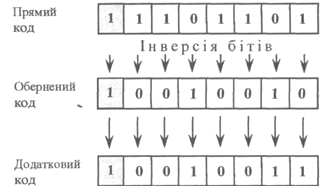
Рисунок 5.1. – Подання від'ємного числа в оберненому і додатковому кодах прямому
Як відомо, цифрові пристрої можуть обробляти тільки інформацію, подану в числовій формі. Під час зчитування документів, текстів програм та інших матеріалів увідні букви кодуються відповідними числами, а у разі виведення їх для читання людиною за кожним числом (кодом символу) будується зображення символу. Відповідність між набором символів і їх кодів називають кодуванням символів.
Зазвичай код символу зберігається в одному байті. Код символу розглядається як число без знака і, отже, може набувати значень від 0 до 255. Такі кодування називають однобайтовими; вони дозволяють використовувати до 256 різних символів. Тепер дедалі більшого поширення набуло двобайтове кодування, за яким коди символів можуть набувати значень від 1 до 65535. У цьому кодуванні є номери для майже всіх застосовуваних символів (букв та ієрогліфів різних мов, математичних, декоративних символів і т. ін.).
Кодування символів зазвичай визначається використовуваною операційною системою чи програмною оболонкою.
Загалом наявність у сучасних цифрових пристроях різних форм і форматів подання чисел дозволяє вибирати ті з них, що найбільшою мірою відповідають вимогам розв'язуваних задач.





