Теоретические основы. Парная регрессия - уравнение связи двух переменных у и х:
Парная регрессия - уравнение связи двух переменных у и х:
где у - зависимая переменная (результативный признак); х - независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии. Линейная регрессии: Нелинейные регрессии делятся на два класса (Рис. 1.1): регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Регрессии, нелинейные по объясняющим переменным: • полиномы разных степеней: • равносторонняя гипербола у = а + Регрессии, нелинейные по оцениваемым параметрам: • степенная • показательная y = • экспоненциальная у = Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических
Рис. 1.1. Основные типы кривых, используемые при количественной оценке связей между двумя переменными.
Последний график неверен! Основное свойство МНК: из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.2):
Рис. 1.2. Линия регрессии с минимальной дисперсией остатков.
Для линейных уравнений регрессии вида
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции rху для линейной регрессии (-1 ≤ rху ≤ 1):
rху =
и индекс корреляции
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
Допустимый предел значений Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:
Средний коэффициент эластичности
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Таблица 1.
|


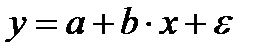
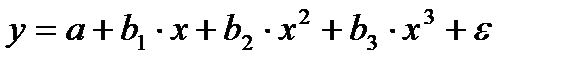

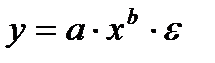 ;
;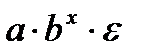 ;
;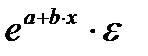
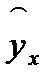 минимальна, т.е.
минимальна, т.е.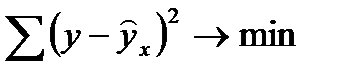
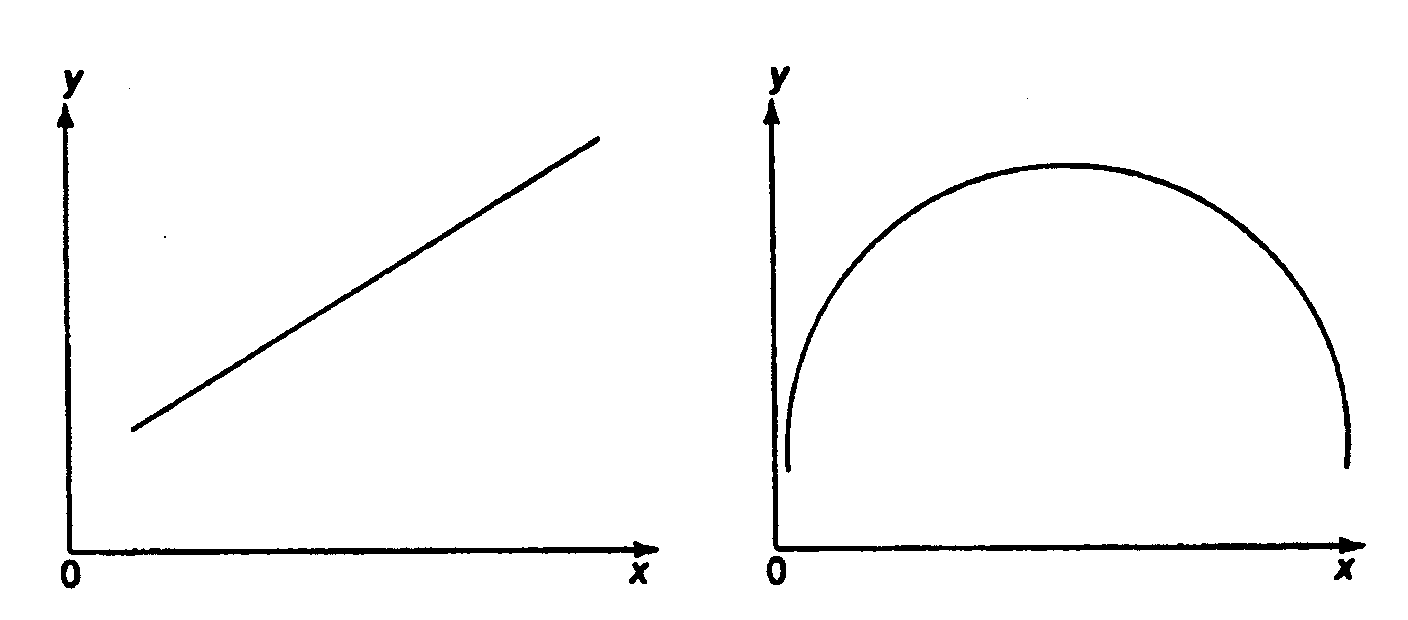
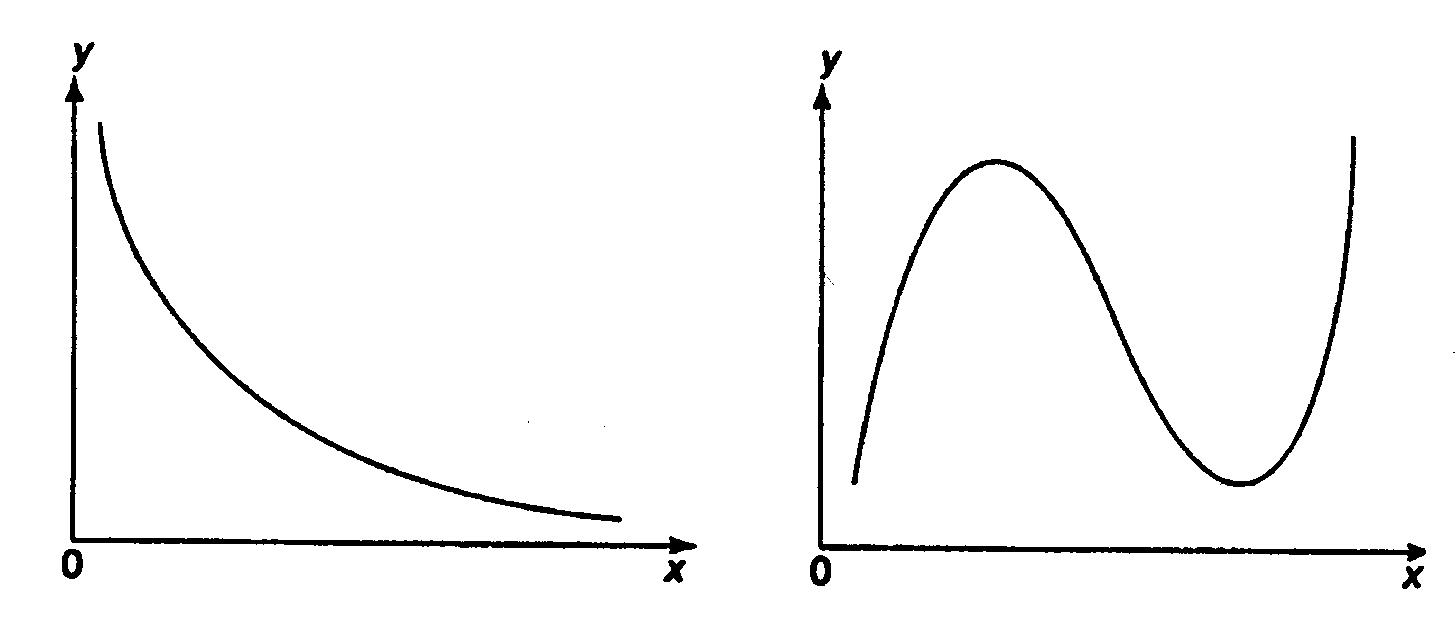
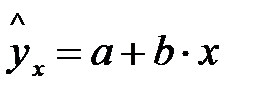
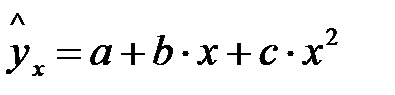

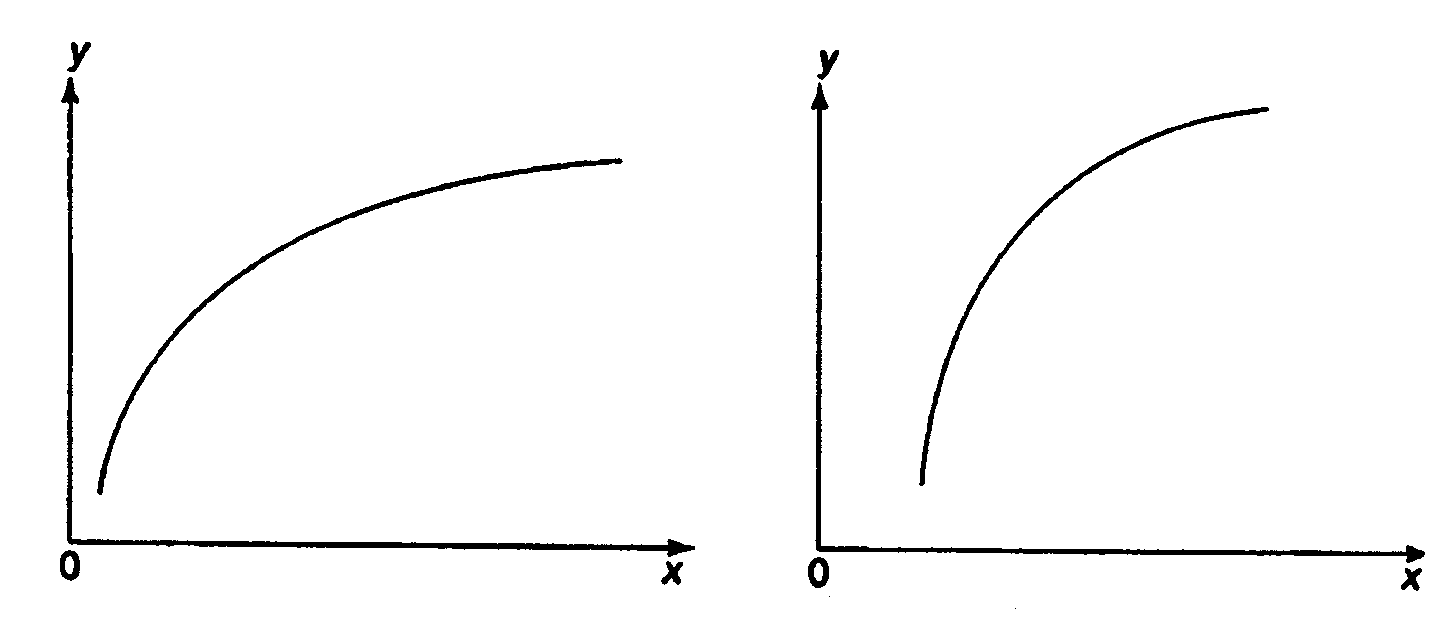
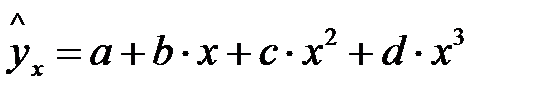
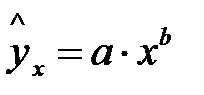


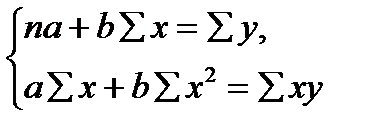

 .
.
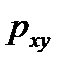 - для нелинейной регрессии (0 ≤ рху ≤ 1):
- для нелинейной регрессии (0 ≤ рху ≤ 1):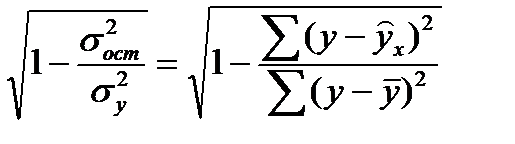 .
.
 - не более 8 - 10%.
- не более 8 - 10%. .
.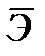 показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора на 1% от своего среднего значения:
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора на 1% от своего среднего значения: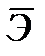 =f '(х)
=f '(х) 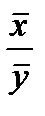
 , то обычно рассчитывается средний коэффициент эластичности
, то обычно рассчитывается средний коэффициент эластичности


