Помощью предложных спектров Н.А. Морозова
При изучение прозаических произведений на уроках литературы рассматриваются прежде всего такие содержательные параметры как сюжет, идейная направленность, характеры и поступки героев, основная мысль произведения, тема и т.д.; и, как правило, не обращается внимания на языковые средства выражения содержательных характеристик. Действительно, любой текст, представленный средствами естественного языка, есть набор букв, из которых формируются слова, а из последних строятся предложения. Слова делятся на неделимые единицы, обилие которых в словах и предложениях позволяют с одной стороны каждому человеку при построение предложений выдерживать индивидуальность, а с другой стороны каждую индивидуальность речи можно отличать формальными математическими характеристиками текста. На это обстоятельство впервые обратил внимание выдающийся русский учёный – энциклопедист Морозов Н.А. (1854-1946г). Вот, что он писал в статье [1]: «Каждый литературно-образованный» человек знает, что все оригинальные авторы отличаются своим складом речи, даже и в том случае, когда мы сравниваем их с писателями того же самого поколения. Мы, русские, легко отличаем, например, склад речи Гоголя от склада речи Пушкина или Тургенева. В английской литература склад речи Теккерея совсем не похож на склад речи Диккенса». … «Чтобы выяснить сразу, что я хочу здесь сказать, рассмотрю несколько примеров. Возьмём хотя бы в нашем русском языке два легко заменяемых друг другом слова: «так как» и «потому что». Почти в каждой фразе одно из них можно заменить другим с сохранением первоначального смысла, и потому в переводе на иностранный язык такое различие в складе речи исчезает, между тем как в оригинале одни авторы могут машинально употреблять почти исключительно первую из этих «служебных частиц речи», редко вспоминая о существовании второй, другие же авторы понии второй, другие же авторы паи второй, другие же авторы поступять совершенно наоборотем как в оригинале одни авторы могут машступят совершенно наоборот». По мнению Морозова Н.А. служебные частицы распоряжаются нашей речью и их он назвал распорядительными частицами, с помощью которых можно различать особенности склада речи писателя. Рассматривая вопрос о том, какие слова могут определять индивидуальность склада речи, он обратил внимание на то, что такие группы слов, как имена существительные, прилагательные и глаголы зависят от содержания текста и частота их употребления ничего не скажет об индивидуальности автора. Однако, по мнению Морозова Н.А.: «даже и при разнородности сюжетов, есть во всех языках ряд слов, которые употребляются почти одинаково во всех родах литературы и которые по своему характеру могут быть названы, как я уже выражался ранее, служебными или распорядительными частицами человеческой речи». Говоря конкретно об указанных частицах, он писал следующее [1]: «Это, прежде всего союзы, предлоги и отчасти местоимения и наречия, а затем и некоторые вставные словечки, в роде: «т.е.», «например» или «и так далее». Затем идут деепричастные и причастные окончания, как задние приставные частицы, характеризующие среднюю сложность фразы у того или другого автора. Даже и самые знаки препинания могут быть названы в этом случае попутными (или паузными) распорядительными частицами всех человеческих языков». Далее Морозов здесь же задает такой вопрос: «Нельзя ли по частоте таких частиц узнавать авторов, как будто по чертам их портретов?» На этот вопрос он отвечает так: «Для этого, прежде всего надо перевести их на графики, обозначая каждую распорядительную частицу на горизонтальной линии, а число ее повторения на вертикальной, и сравнить эти графики между собой у различных авторов». Подобные графики Морозов Н.А. назвал лингвистическими спектрами, а исследование различных текстов с их помощью - лингвистическим анализом. Технология этого анализа, предложенная Морозовым Н.А., такова: отсчитывается первая тысяча слов любого текста и затем подсчитывается число встретившейся той или иной служебной частицы. Чтобы упростить спектры, Морозов Н.А. разделил их на предложные, союзные и местоименные. По его подсчетам оказалось, что часто повторяющимися у всех русских авторов оказались предлоги в, на, с, поэтому их графики им были названы главным предложным спектром. Например, на тысячу слов у Гоголя предлог в повторялся в «Тарасе Бульбе» 23 раза, в «Майской ночи» - 15, а в «Страшной мести» - 16 раз; предлог на повторился 24 раза в «Майской ночи» и 26 раз в «Тарасе Бульбе» и «Страшной мести». Когда же значения частот рассматриваемых предлогов на указанных графиках были соединены прямыми линиями, то во всех трех рассматриваемых произведениях Гоголя получились довольно сходные ломаные линии. В произведениях же Пушкина - «Барышня-крестьянка», «Дубровский», «Капитанская дочка» характер таким же образом построенных ломаных оказался другим. Статья [1] была опубликована в 1915 году. Через некоторое время появилась статья известного русского математика Маркова А.А. (старшего) [2], в которой лингвистический анализ Морозова Н.А. был подвергнут резкой критике. Суть критики Маркова А.А. сводилась к следующему. Если для подсчёта частоты той или иной служебной частицы брать исследуемые 1000 слов текста в разных местах одного и того же произведения, то частота появления данной частицы может резко измениться, что в свою очередь изменит характер лингвистического спектра. В тот период времени все расчёты частотного анализа производились «вручную» и подтвердить или опровергнуть критику маститого математика Маркова В.А. не представлялось возможным. Современные же компьютерные технологии позволяют проверить опасения Маркова А.А. Для этого постулируем следующую гипотезу. Поиск числа повторений той или иной служебной частицы среди тысячи слов исследуемого текста отождествим с известной задачей математической статистики о повторение испытаний, т.е. количество слов текста будем считать числом испытаний ni, а число mi повторений частицы – числом появлений события. Тогда можно ввести понятие частоты
как отношение указанных чисел. В математической статистике известны случаи, когда при увеличении числа испытаний числовые значения частот колеблются около некоторой величины и отклонения частот от указанной величины уменьшаются с ростом числа испытаний. Как правило, в качестве таковой величины принимается среднее арифметическое Pср частот Pi. Если в формуле (1) символом i будем обозначать номер серии испытаний, то Pср необходимо вычислять так:
где N – число серий. В статистике описанный факт повторяемости частот называется законом устойчивости частот, а на основе известной теоремы Я. Бернулли, величина Pср принимается в качестве вероятности появления разыскиваемого события. Если для всех служебных частиц будет иметь место закон устойчивости частот, то критику Маркова А.А. следует признать несостоятельной. Для выявления закона устойчивости частот применительно к главному предложному спектру (в, на, с) весь рассматриваемый текст разделим на фрагменты из тысячи слов. Далее начинаем разыскивать число повторений каждого предлога данного спектра в первой тысячи слов. В этом случае число испытаний n1 = 1000 назовём первой серией испытаний, а получившееся число m1 повторений данной служебной частицы следует считать числом появлений разыскиваемого события. Теперь по формуле (1) можно вычислить частоту P1 первой серии испытаний. Для получения частоты P2 второй серии, необходимо к первому фрагменту текста добавить второй и для n2 = 2000 с учётом нового значения m2 вычислить P2 по (1). Указанный процесс продолжить до тех пор, пока указанным анализом не будет охвачен весь исследуемый текст. Полученный таким образом набор чисел Pi покажет, имеет ли место закон устойчивости частот. Если закон устойчивости частот будет иметь место, то среднюю частоту Pср характеризующую вероятность появления данной служебной частицы вычислим по формуле (2). Реализацию описанного выше алгоритма продемонстрируем на произведении Н.В. Гоголя «Страшная месть» с помощью информационных технологий. Для этого в сети Интернет с помощью поисковой системы Рамблер найдём текст данного произведения в электронной форме, для чего воспользуемся специализированной программой-браузером Internet Explorer. После запуска Internet Explorer введём в его адресную строку, следующую запись «www.rambler.ru» и выполним однократное нажатие клавиши Ввод (Enter) на клавиатуре. В результате этих действий в окне программы Internet Explorer отобразиться Web-страница поисковой системы Рамблер. Далее, на отобразившейся странице, в строке поиска введём запрос «Страшная месть Гоголь», подведём указатель мыши к кнопке «Поиск» и выполним однократное нажатие левой клавиши мыши. После этого, поисковая система Рамблер проведёт поиск сайтов, удовлетворяющих условию нашего запроса и отобразит их список в порядке уменьшения популярности. Выберем один из ресурсов, расположенных вначале полученного списка и перейдём на него, для чего подведём курсор мыши к названию этого ресурса и выполним однократное нажатие левой клавиши мыши. После перехода на страницы выбранного ресурса, найдём на них ссылку на документ, содержащий текст произведения Н.В. Гоголя «Страшная месть» и загрузим его на локальный компьютер, на котором планируется проведение его анализа с помощью вышеуказанного алгоритма. Для этого подведём курсор мыши к найденной ссылке и выполним однократное нажатие правой клавиши мыши. Далее, в появившемся контекстном меню, подведём курсор мыши к команде «Сохранить как» и выполним однократное нажатие левой клавиши мыши. Документ будет сохранён в указанную нами папку на локальном компьютере. Теперь, имея в наличие электронную версию произведения Н.В. Гоголя «Страшная месть» проведём его анализ, используя вышеописанный алгоритм. Для чего, первоначально, преобразуем, текст данного произведения таким образом, чтобы на каждой строке документа, содержащего данный текст, находилось лишь одно слово или предлог, что необходимо для проведения расчётов с использованием программы Microsoft Excel. Для этого воспользуемся редактором Microsoft Word из пакета Microsoft Office. После запуска Microsoft Word откроем в нём документ, содержащий текст анализируемого нами произведения. После этого подведём курсор мыши к имени меню «Правка» расположенного в строке главное меню Microsoft Word и выполним однократное нажатие левой клавиши мыши. В открывшемся каскадном меню подведём курсор мыши к команде «Заменить» и выполним однократное нажатие левой клавиши мыши. Далее, в появившемся диалоговом окне «Найти и заменить» в текстовое поле «Найти» введём символ пробел, а в текстовое поле «Заменить на» служебный символ «^p». После чего подведём курсор мыши к кнопке «Заменить всё» и выполним однократное нажатие левой клавиши мыши. В результате проделанных действий, получим документ, содержащий текст произведения Н.В. Гоголя «Страшная месть», в котором на каждой строке документа находится лишь одно слово или предлог. Для проведения дальнейшего анализа по указанному выше алгоритму, перенесём преобразованный текст в программу Microsoft Excel, для чего скопируем его в буфер обмена в программе Microsoft Word, откроем программу Microsoft Excel, активизируем ячейку A1 на Листе 1 рабочей книги Excel и выполним вставку из буфера обмена. Теперь, проведём подсчёт абсолютных величин появления элементов главного предложного спектра (в, на, с) в анализируемом тексте учитывая, что количество ni в каждой серии испытаний изменяется согласно приведенному выше алгоритму. Для этого воспользуемся существующей в программе Microsoft Excel статистической функцией «СЧЁТЕСЛИ». В качестве первого аргумента функции будем использовать значение ni для каждой серии испытаний. В качестве второго аргумента, будем использовать, элементы главного предложного спектра (в, на, с). В результате проведения расчетов с использованием статистической функции «СЧЁТЕСЛИ» получим ряд значений числа mi появлений элементов главного предложного спектра в произведение Н.В. Гоголя «Страшная месть» для каждой серии испытаний. После чего вычислим с помощью программы Excel значения частоты Pi для каждой серии испытаний по формуле (1). Далее, проведём анализа поведения числовых значений частот появления рассматриваемых предлогов в каждой серии испытаний, из которого определим, что для элементов данного предложного спектра имеет место закон устойчивости частот. Этот факт позволит провести вычисления Pср по формуле (2) и принять их в качестве вероятностей появления элементов изучаемого спектра. После чего, проиллюстрируем установленный закон устойчивости частот с помощью графиков, отображающих поведение значений Pi в зависимости от номера серии i испытаний. Перейдём к реализации описанного выше алгоритма, для произведения Н.В. Гоголя «Страшная месть», для чего напишем программу на языке макрокоманд. Так как любая программа требует отладки, будем проводить её посредствам сравнения получающихся в процессе написания программы результатов с образцами, представленными в виде рисунков.
1. Включение компьютера и вход в систему. Результат выполнения представлен на рисунке 1.
Рис. 1.
Результат выполнения представлен на рисунке 2.
Рис. 2.
Параметры: - адрес: «http: //www.rambler.ru/» Результат выполнения представлен на рисунке 3.
Рис. 3.
4. Поиск Web-ресурса с помощью поисковой системы Rambler. Параметры: - запрос: «Страшная месть Гоголь» Результат выполнения частично представлен на рисунке 4.
Рис. 4.
5. Открытие Web-страницы – переход по ссылке. Параметры: - ссылка: «Библиотека Комарова | Н. В. Гоголь. Страшная месть» Результат выполнения представлен на рисунке 5.
Рис. 5.
6. Загрузка файла с помощью программы Microsoft Internet Explorer. Параметры: - ссылка: «Текст»; - папка: «Мои документы»; - имя файла: «Гоголь - Страшная месть.doc»
7. Запуск программы Microsoft Word. Результат выполнения представлен на рисунке 6.
Рис. 6.
8. Открытие документа Microsoft Word. Параметры: - имя файла: «Страшная месть.doc». Результат выполнения представлен на рисунке 7.
Рис. 7.
9. Замена символов в документе Microsoft Word. Параметры: - заменяемый символ: «»; - заменяющий символ: «^p». Результат выполнения представлен на рисунке 8. Рис. 8.
10. Копирование в буфер обмена Microsoft Word.
11. Запуск программы Microsoft Excel. Параметры: - рабочий стол. Результат выполнения представлен на рисунке 9.
Рис. 9.
Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 10. Рис. 10.
Параметры: - ячейка: A1. Результат выполнения представлен на рисунке 11.
Рис. 11.
Параметры: - ячейка: B1; - данные: 1000. Результат выполнения представлен на рисунке 12.
Рис. 12.
Параметры: - ячейка: B2; - данные: «=B1+1000» - конечная ячейка: B13. Результат выполнения частично представлен в таблице на рисунке 13.
Рис. 13
Параметры: - ячейка: С1; - данные: «=СЧЁТЕСЛИ($A$1: $A$1000; " в")». Результат выполнения представлен на рисунке 15.
Рис. 14.
Параметры: - ячейка: D1; - данные: «=СЧЁТЕСЛИ($A$1: $A$1000; " на")». Результат выполнения представлен на рисунке 16.
Рис. 16.
Параметры: - ячейка: E1; - данные: «=СЧЁТЕСЛИ($A$1: $A$1000; " с")». Результат выполнения представлен на рисунке 17.
Рис. 17.
Повторим шаги 16 – 18 до строки 13 для столбцов C, D, E изменяя в формулах значение $A$1000 на $A$2000, $A$3000 … $A$13000 соответственно. Результат последовательного выполнения шагов 16 – 18 для столбцов C, D, E частично представлен на рисунке 18. Рис. 18.
18. Автозаполнение - формула. Параметры: - ячейка: F1; - данные: «=C1/B1»; - конечная ячейка: H13. Результат выполнения частично представлен в таблице на рисунке 19. Рис. 19.
19. Автозаполнение - формула. Параметры: - ячейка: I1; - данные: «=СУММ(F$1: F$13)/13»; - конечная ячейка: K13. Результат последовательно выполнения описанных выше шагов представлен на рисунке в таблице 1.
Таблица 1
Параметры: - диапазон ячеек 1: F: F; - диапазон ячеек 2: I: I. Результат выполнения представлен в таблице на рисунке 20. Рис. 20. 21. Построение диаграммы. Параметры: - тип: «график»; - вид: «первый»; - название оси Х: «i»; - название оси Y: «Pi». Результат выполнения представлен на рисунке 26.
Рис. 26. Иллюстрация закона устойчивости частот для предлога в в произведении Н.В. Гоголя «Страшная месть»
Параметры: - диапазон ячеек 1: G: G; - диапазон ячеек 2: J: J. Результат выполнения представлен в таблице на рисунке 27.
Рис. 27.
23. Построение диаграммы. Параметры: - тип: «график»; - вид: «первый»; - название оси Х: «i»; - название оси Y: «Pi». Результат выполнения представлен на рисунке 28.
Рис. 28. Иллюстрация закона устойчивости частот для предлога на в произведении Н.В. Гоголя «Страшная месть»
24. Активизация не связанного диапазона ячеек.
Рис. 29. 25. Построение диаграммы. Параметры: - тип: «график»; - вид: «первый»; - название оси Х: «i»; - название оси Y: «Pi». Результат выполнения представлен на рисунке 30.
Рис. 30. Иллюстрация закона устойчивости частот для предлога с в произведении Н.В. Гоголя «Страшная месть»
26. Сохранение файла в сетевую папку. Параметры: - сетевая папка: «//Public»; - имя файла: «Гоголь – Страшная месть.xls».
|
, (1)
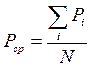, (2)
2. Запуск программы Microsoft Internet Explorer.
3. Открытие Web-страницы – ввод адреса.
12. Выбор активного листа.
13. Вставка из буфера обмена Microsoft Excel.
14. Занесение целых чисел в ячейку.
15. Автозаполнение - формула.
16. Занесение формул в ячейку.
17. Занесение формул в ячейку.
18. Занесение формул в ячейку.
20. Активизация не связанного диапазона ячеек.
22. Активизация не связанного диапазона ячеек.
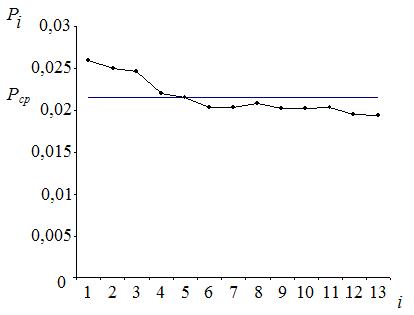
Параметры: - диапазон ячеек 1: H: H; - диапазон ячеек 2: K: K. Результат выполнения представлен в таблице на рисунке 29.
