Частотный анализ звуков русских народных песен
Михайлова Светлана Петровна
Музыкальное произведение, записанное при помощи графических знаков, будь то ноты или буквенные символы, являет собой двуединство формы и содержания. Так же как в языке, в музыке аудио информация может быть представлена с помощью графических символов. История становления музыкального письма берет свое начало еще от античной древности. В эпоху раннего средневековья была распространена буквенная запись звуков. Она позволяла обозначить лишь высоту звуков, но их длительность при этом не фиксировалась вовсе. Со временем этот способ записи нот оказался мало пригодным для записи начавшей развиваться в то время многоголосной музыки.
Название музыкальных звуков основано на начальных слогах первых шести строчек средневекового римско-католического гимна в честь св. Иоанна (легендарного покровителя певцов), сочиненного около 700-го года Павлом Диаконом: Ut queant la xis Re sonare fibris Mi ra gestorum Fa muli tuorum Sol ve poluti La bii reatum, Sancte Johannes. Звук си был добавлен позднее.
В настоящий момент в основном используются 2 системы записи музыкальных произведений – нотная и буквенная (приведена ниже).
Математизация музыки началась с эпохой «механического композитора». В 1757 году, в Германии было издано другое руководство для сочинения музыки немузыкальными средствами. Автор его И.Ф.Кирнбергер. Называлось оно «Руководство к сочинению полонезов и менуэтов с помощью игральных костей». Автор составил специальную таблицу, она состояла из шести занумерованных колонок и восьми строк. Возле каждой колонки стояла цифра, соответствующая одной из цифр на грани кости. А каждой строке соответствовал такт сочинения. В клетке таблицы автор записывал какую-то сочиненную им комбинацию нот. Бросок игральной кости давал случайное число от 1 до 6. Допустим, выпала цифра 4. Тогда в клетке на пересечении колонки с номером 4 и первой строки (первого такта) находили комбинацию нот, которая и считалась первым тактом менуэта. Потом кости бросали еще и еще, до последнего, восьмого такта - тогда менуэт считался законченным. Нетрудно подсчитать, что количество различных вариантов восьми тактового менуэта составляет 68. Это 1 679616 вариантов. При сочинении шестнадцати тактовой пьесы число возрастает до 616, то есть 2821 109907456 - почти до 3 триллионов. Математики, изучающие музыку, нашли, что в популярных песнях содержится от 35 до 60 нот. Статистический анализ большого числа песен показал, что структура их такова: имеется одна часть, назовем ее А, охватывающая восемь тактов и содержащая от 18 до 25 нот. Эта часть повторяется. За ней следует часть В, она тоже содержит восемь тактов, но состоит из 17-35 нот. После нее повторяется снова часть А. Удалось установить и другие интересные закономерности. Если пять нот идут последовательно вверх, то шестая обязательно идет вниз, и наоборот. Другая закономерность: первая нота в части А обычно не является второй, четвертой или пятой минорной нотой в шкале. В песнях соблюдаются и правила композиции, такие, как правила Моцарта: никогда интервал между соседними нотами не должен превышать шести тонов. Каждому, наверное, удавалось, слушая мелодию – иногда совершенно незнакомую, – угадывать следующую ноту. Чаще всего это случается с лирическими песнями. Специалисты о них говорят, что каждая последующая нота здесь несет меньше информации, чем, например, в музыке Прокофьева и Шостаковича, где мелодии насыщены неожиданными оборотами. Выходит, что и количество информации на одну ноту – численная величина, параметр, по которому можно судить о музыке. При проведении информационных измерений в музыкальных произведениях, последнее можно считать набором (множеством) нотных знаков. Наиболее доступен простой анализ «по наличию», не учитывающий длительность и высоту звуков. При этом каждый элемент множества приводится в соответствие с числами натурального ряда, в результате чего получается конечное множество, над элементами которого можно производить измерения. Возьмем формулы, применяемые для расчета энтропии поэтического текста. Общее число нот произведения обозначим N1 , а количество конкретной i-ой ноты – Ni. Рассчитаем частоту появления конкретной ноты в произведении по формуле
При расчете энтропии информации применим формулу Шеннона, обозначив энтропию Н2
Определим Н2 для нескольких русских народных песен:
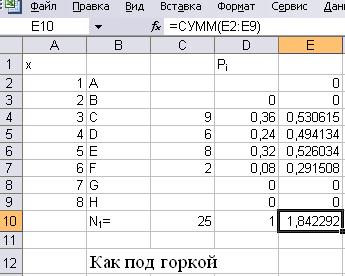
Результаты расчетов для песни «Как под горкой»:
Далее в таблице приведены результаты обработки 10 песен
Уже из приведенных данных видно, что используются в народных мотивах не все ноты сразу, что резко отличает их от авторских композиций. Более того, наиболее раннее произведение отличает наименьшее значение Н, а самое позднее по времени создания – наибольшее значение Н. Это ярко иллюстрирует развитие устного народного творчества, расширение мелодического образа народной музыки. Теперь попробуем определить наиболее часто используемую ноту, звук, который является стержнем. 8 из 10 рассматриваемых песен тональности до-мажор. Логично предположить, что основой будет являться нота до. Так ли это?
Рассчитаем суммарное значение частоты нот:
Расположим данные в порядке возрастания:
Из результатов видно, что максимальное количество частот распределяется на 3 ноты – до, ми и соль, которые составляют тоническое трезвучие тональности до-мажор.
Определим минимальные и максимальные значения:
Результаты подтверждают приоритетность звуков тонического трезвучия в мелодии русских народных песен. Таким образом, мы определили опорные звуки песен, по которым можно сделать вывод о тональности и по которым возможно построение аккордового сопровождения по законам гармонизации. Подобный анализ уместен при обработке народной музыки, так как облегчает определение тональности, а следовательно, и фиксацию произведения с помощью нот.
Источники: 1. Злотина Э. С. Синтез интуитивного и системного в творчестве. - Методология и методы технического творчества. – Новосибирск, 1984.с.9-14 2. Злотина Э.С. Закономерности развития музыкальных форм.Л.: 1985.Журнал «Технология творчества», №1 1999. http: //www.trizminsk.org/e/245003.htm 3. Информатика и математика: Программа для студентов гуманитарных факультетов./ Под ред. В.А.Бубнова М.: МГПУ, 2005, 270с. 4. Калмыков Б., Фридкин Г. Сольфеджио. Часть 1. Одноголосие. – Москва, 1992, 107 с.
|

 В период с VIII по XI век, начала использоваться так называемая невменная запись(Невмы - от греч. neuma - графические значки, помещавшиеся над словесным текстом), но она была весьма не совершенной, так как не фиксировала точных звуковых соотношений, а лишь указывала (правда, достаточно наглядно) направление развития мелодии. Древнерусским эквивалентом невменного письма были " крюки" или " знамёна". Древнейшие памятники русского крюкового письма относятся к концу XI-начало XII века. Со временем в целях совершенствования невменного письма - для точной фиксации высоты звуков - к невмам справа стали добавлять буквенные обозначения.
В период с VIII по XI век, начала использоваться так называемая невменная запись(Невмы - от греч. neuma - графические значки, помещавшиеся над словесным текстом), но она была весьма не совершенной, так как не фиксировала точных звуковых соотношений, а лишь указывала (правда, достаточно наглядно) направление развития мелодии. Древнерусским эквивалентом невменного письма были " крюки" или " знамёна". Древнейшие памятники русского крюкового письма относятся к концу XI-начало XII века. Со временем в целях совершенствования невменного письма - для точной фиксации высоты звуков - к невмам справа стали добавлять буквенные обозначения. Подлинную реформу, приведшую в итоге к образованию современной системы нотного письма, совершил монах бенедиктинец Гвидо Аретинский (ок. 995-1050 гг.). Вместо невм стали писать на линиях и между ними квадратные ноты (возникло так называемое хоральное письмо), а в целом нотная запись значительно упростилась и приобрела необходимую для чтения наглядность. В Западной Европе в конце XII-начале XIII века была изобретена так называемая мензуральная нотация. Во второй половине XVII века итальянским теоретиком Бонончини (1642-1678) неудобный для распевания слог ut (ут) был заменен на слог До. С того времени и поныне мы имеем знакомые всем До, Ре, Ми, Фа, Соль, Ля, Си.
Подлинную реформу, приведшую в итоге к образованию современной системы нотного письма, совершил монах бенедиктинец Гвидо Аретинский (ок. 995-1050 гг.). Вместо невм стали писать на линиях и между ними квадратные ноты (возникло так называемое хоральное письмо), а в целом нотная запись значительно упростилась и приобрела необходимую для чтения наглядность. В Западной Европе в конце XII-начале XIII века была изобретена так называемая мензуральная нотация. Во второй половине XVII века итальянским теоретиком Бонончини (1642-1678) неудобный для распевания слог ut (ут) был заменен на слог До. С того времени и поныне мы имеем знакомые всем До, Ре, Ми, Фа, Соль, Ля, Си. .
.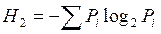 .
.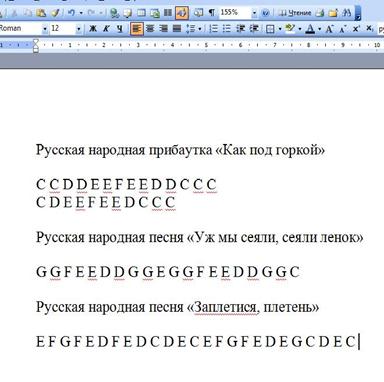 Для этого необходимо отсканировать буквенные записи песен. И перенести данные в программу Microsoft Word. Далее необходимо, по аналогии с проведением частотного анализа поэтических текстов по всем буквам, провести первичную подготовку в программе MS Excel. Устанавливаем соответствие между числами натурального ряда и буквенными обозначениями нот. При этом номер ноты будет отождествляться с переменной величиной X. В ячейки столбца C вносится информация о количестве букв, указанных в столбце B. Далее производится расчет, при котором значение N1 будет выведен в ячейке С10, а значение Н2 в ячейке Е10.
Для этого необходимо отсканировать буквенные записи песен. И перенести данные в программу Microsoft Word. Далее необходимо, по аналогии с проведением частотного анализа поэтических текстов по всем буквам, провести первичную подготовку в программе MS Excel. Устанавливаем соответствие между числами натурального ряда и буквенными обозначениями нот. При этом номер ноты будет отождествляться с переменной величиной X. В ячейки столбца C вносится информация о количестве букв, указанных в столбце B. Далее производится расчет, при котором значение N1 будет выведен в ячейке С10, а значение Н2 в ячейке Е10.