Организация циклов
Циклом называется многократно повторяющаяся последовательность действий (операторов). Цикл – типичная структура, характерная для программ, реализуемых на компьютере. Средства языка C# для организации циклов приводятся в п. 1.7.2, 1.7.3, 1.7.4. 2.1.1. Циклы по счетчику Рассмотрим вначале циклы по счетчику, т.е. когда количество повторений цикла известно до начала его выполнения. При организации цикла по счетчику необходимо: 1) выделить повторяющиеся действия и записать их в общем виде; 2) выбрать управляющую переменную цикла. Это может быть какая-либо величина, имеющаяся в постановке задачи, либо используемая специально в качестве счетчика; 3) определить параметры цикла, т.е. начальное и конечное значения управляющей переменной и шаг ее изменения. Пример 2.1. Пусть требуется вычислить сумму S = 1 + 2 + 3 + … +100. Организуем вычисления так, чтобы на каждом шаге выполнялись простые действия, в данном случае это прибавление к сумме очередного слагаемого. Вначале необходимо обнулить переменную, в которой будет накапливаться сумма (s = 0), а затем на каждом шаге добавлять к сумме очередной член, т.е. многократно выполнять операцию s = s + i, где i = 1, 2, 3,..., 100. Таким образом, в качестве управляющей переменной цикла в данном случае можно использовать сам член суммы, который изменяется в заданных пределах (от 1 до 100) с заданным шагом 1. Тогда программа будет иметь следующий вид: using System; namespace ConsoleApplication3 { class Program { static void Main(string[] args) { int i, s = 0; for (i = 1; i < = 100; i = i + 1) s = s + i; Console.WriteLine(" s = {0}", s); Console.ReadKey(); } } } Результат выполнения программы.
Пример 2.2. Вычислить сумму четных чисел от 2 до 20. Здесь требуется организация цикла по счетчику с управляющей переменной, например, k, изменяющейся с шагом 2 от 2 до 20. using System; namespace ConsoleApplication1 { class Program { static void Main() { int k, s = 0; for (k = 2; k < = 20; k = k + 2) s = s + k; Console.WriteLine(" s= {0}", s); Console.ReadKey(); } } } Или namespace ConsoleApplication1 { class Program { static void Main(string[] args) { int k = 2, s = 0; do { s = s + k; k = k + 2; } while (k < = 20); Console.WriteLine(" s = {0}", s); Console.ReadKey(); } } } Пример 2.3. Вычислить сумму s = 3 + 32 + 33 + … + 38. На каждом шаге алгоритма необходимо прибавлять к сумме очередное слагаемое (s = s + 3i), где i = 1, 2, 3,..., 8. Вспомним, что операция возведения в степень в языке C# отсутствует, поэтому следующий член суммы будем получать из предыдущего домножением его на 3. В качестве управляющей переменной цикла можно использовать показатель степени, изменяющийся в заданных пределах от 1 до 8 с заданным шагом, равным 1. Программа, таким образом, будет иметь следующий вид (здесь и далее приводится только алгоритмическая часть проекта): int s = 0, a = 1; for (int i = 1; i < = 8; i = i + 1) { a = a * 3; s = s + a; } Console.WriteLine(" s = {0}", s); Console.ReadKey(); Замечание. Выражение для получения очередного члена последовательности из предыдущего называется рекуррентной формулой. Пример 2.4. Вычислить s = 5/8 + 7/10 +... + 31/34. Для организации цикла в этом случае можно использовать числитель, изменяющийся от 5 до 31 с шагом 2, а знаменатель выразить через числитель (он отличается от числителя на 3): double s = 0; for (int a = 5; a < = 31; a = a + 2) { s = s + a / (a + 3.0); } Console.WriteLine(" s = {0}", s); Console.ReadKey();
Замечание. При делении целого на целое результат получается целый (дробная часть теряется). Поэтому при вычислении знаменателя второе слагаемое записано в виде вещественного числа. Знаменатель будет теперь иметь тип double, и результат деления будет иметь тип double. Возможны и другие способы организации вычислений. Предложите их самостоятельно. Для организации цикла в данном примере можно использовать специальную переменную (счетчик), определяющую номер итерации. Для определения общего количества повторений цикла (n) можно использовать формулу n = (iкон – iнач)/h+1. В данном случае при iкон = 31, iнач = 5, h = 2 получаем n = 14. Тогда программа будет иметь вид double s = 0, a; int n; double xh = 5, xk = 31, h = 2; a = xh; n = (int)((xk - xh) / h + 1); for (int i = 1; i < = n; i = i + 1) { s = s + a / (a + 3); a = a + h; } Console.WriteLine(" s = {0}", s); Console.ReadKey(); Здесь при вычислении n использовано явное преобразование типа указанием типа в скобках перед выражением, т.к. результат метода Round (округление) имеет тип double.
Пример 2.5. Вычислить double s = 0.0, a; int i, p = 1; for (i = 1; i < = 25; i = i + 1) { p = -p; a = p * 2 * i / (i * i + 2.0); s = s + a; } s = (2.0 / 3.0) * s; Console.WriteLine(" {0: f4}", s); Console.ReadKey();
Замечание. В программе использован тот же прием согласования типов, что и в предыдущем примере. Порядок вычислений и тип результата операций в выражении правой части при вычислении члена суммы a следующий: вычисляется p * 2 – тип результата int, результат этой операции умножается на i, тип результата int, вычисляется знаменатель (выражение в скобках) в следующем порядке: вычисляется i * i - результат операции имеет тип int и к этому результату прибавляется вещественное число 2.0 (по умолчанию типа double), знаменатель после вычисления имеет тип double. Таким образом значение выражения правой части имеет тип double. Пример 2.6. Получить таблицу значений функции const double xh = -2.5, xk = 2.5, h = 0.5; double x, y; int i, n; n = (int)((xk - xh) / h + 1); x = xh; for (i = 1; i < = n; i = i + 1) { y = Math.Pow(x, 2) + 0.5 * x; Console.WriteLine(" x = {0: f2}\ty = {1: f2}", x, y); x = x + h; } Console.ReadKey();
Замечания. 1. Здесь для определения количества значений аргумента при его изменении в пределах от xh до xk c шагом h использована формула n =(xk - xh)/h + 1.В программе для получения в качестве n целого значения использовано явное преобразование типа указанием его в скобках перед выражением. 2. Для вычисления 3. Наличие символа \t в строке формата обеспечивает табуляцию при выводе каждого значения y, что обеспечивает большую наглядность результата. (Этого эффекта можно добиться и другими способами. Предложите их самостоятельно.) Второй вариант программы. Используется цикл do. const double xh = -2.5, xk = 2.5, h = 0.5; double x, y; x = xh; do { y = Math.Pow(x, 2) + 0.5 * x; Console.WriteLine(" x = {0: f2}\ty = {1: f2}", x, y); x = x + h; } while (x < xk + 0.0001); Console.ReadKey(); Здесь при проверке условия while сравнение текущего значения x осуществляется с величиной несколько большей верхней границы его изменения. Это связано с особенностями представления в памяти компьютера вещественных чисел. Вещественные числа представляются неточно и в результате многократного выполнения арифметических операций может накопиться ошибка, так что последнее значение x может быть несколько больше xk и при отсутствии второго слагаемого в условии не попадет в таблицу. Пример 2.7. Вычислить p = n! при n = 8. Вычисление факториала можно организовать в цикле, домножая каждый раз значение p на очередной сомножитель. const int n = 8; int p = 1; for (int i = 2; i < = n; i++) { p = p * i; } Console.WriteLine(" p = {0: d}", p); Console.ReadKey();
2.1.2. Циклы по условию Циклы по условию необходимо организовывать, когда количество повторений цикла неизвестно и в ряде случаев является искомой величиной при решении задачи. Средства языка C# для организации циклов по условию приведены в п. ……. Пример 2.8. Определить количество (n) членов арифметической прогрессии
сумма которых впервые превысит заданное число р. На каждом шаге алгоритма нужно добавлять к сумме s очередной член m = a + i*h (s = s + m), i = 1, 2,..., но при этом перед каждым прибавлением очередного члена проверять условие s < = p. Как только в первый раз условие не будет выполнено, т.е. будет s > p, необходимо выйти из цикла. Далее приводится программа для решения задачи при a = 2, h = 3, p = 41. В программе текущее значение номера члена суммы обозначено через n. Значение этой переменной, при котором впервые оказалась s > p, и будет результатом. int s = 0, n = 0, m; const int a = 2, h = 3, p = 41; while (s < = p) { m = a + n * h; s = s + m; n = n + 1; } n = n - 1; //вычитается 1, прибавленная после последнего изменения суммы. Console.WriteLine(" {0: d}", n); Console.ReadKey();
Второй вариант программы использует оператор цикла с проверкой условия после первого прохождения цикла. int s = 0, n = 0, m; const int a = 2, h = 3, p = 41; do { m = a + n*h; s = s + m; n = n + 1; }while(s < = p); n = n - 1; Console.WriteLine(" {0: d}", n); Console.ReadKey(); З а м е ч а н и е. Член суммы m можно было бы вычислять рекуррентно: m = m + h, задав до начала цикла m = a (в программу при этом нужно внести и некоторые другие изменения, которые рекомендуется выполнить самостоятельно). Пример 2.9. Вычислить сумму double x = 0.5; const double eps = 0.0001; double s = 0, a; int n = 1; do { a = Math.Cos(n*x)/n; s = s + a; n = n + 1; }while(Math.Abs(a)> eps); Console.WriteLine(" Сумма равна {0: f4}", s); Console.ReadKey();
Пример 2.10. Методом итераций найти корень уравнения При программной реализации метода итераций нет необходимости в использовании переменных с индексами. Для организации вычислительного процесса необходимо одновременно иметь в памяти значения лишь двух последовательных приближений (обозначим их х0 и х1). Следующее приближение х1 получается из предыдущего х0. Если условие достижения точности аbs(х1–х0)£ При организации цикла проверку условия удобно осуществлять после первого прохождения цикла, т.е. использовать цикл do … while.
double x0 = -0.4; const double eps = 0.0001; double x1, d; do { x1 = 0.5 * (Math.Sin(x0 * x0) - 1); d = Math.Abs(x1 - x0); x0 = x1; }while(d > = eps); Console.WriteLine(" Корень равен {0: f4}", x1); Console.ReadKey();
Пример 2.11. Вычислить частное p и остаток q от деления двух натуральных чисел r и t, не используя операцию деления. Число r можно представить в виде int r, t, q, p = 0; r = 26; t = 8; q = r; while (q > = t) { q = q - t; p = p + 1; } Console.WriteLine(" Частное {0: d} Остаток {1: d}", p, q); Console.ReadKey();
Здесь используется цикл с проверкой условия до первого выполнения тела цикла (что важно), так как возможен случай, когда r < t, и тело цикла не должно выполняться ни разу.
Пример2.12. Корабль должен преодолеть путь в 3000 км. В первый день он прошел 200 км. Каждый следующий день он будет проделывать путь на 5% больше, чем в предыдущий день. Через какое время он прибудет в порт назначения? Обозначим путь одного дня через Р. Вначале Р = 200. Путь следующего дня вычисляется как Р = Р + 0.05Р = 1.05Р. Это значение прибавляем к суммарному пути S: S = S + P. Количество дней обозначим через n и будем увеличивать его каждый раз на 1. double s = 0.0, p = 200.0; int n = 0; while(s < 3000) { s = s + p; n = n + 1; p = p * 1.05; } Console.WriteLine(" {0: d}", n); Console.ReadKey();
2.1.3. Вложенные циклы. Пример 2.13. Вычислить сумму Вначале ограничимся вычислением суммы при заданном значении х. Здесь член суммы необходимо вычислять рекуррентно. Для вывода рекуррентной формулы выпишем выражения для двух последовательных членов суммы, например (i–1)-го и i-го, и, разделив i-ый член на (i–1)-ый, получим выражение, на которое необходимо домножить (i-1)-й член для получения i-го. Итак,
Таким образом, чтобы получить следующий i-й член из предыдущего (i-1)-го члена, его нужно домножить на 2*х/i. Вычисление суммы для фиксированного значения х может быть осуществлено следующим образом: double s, a, x = 0.1; s = 1; a = 1; for (int i = 1; i < = 12; i++) { a = a * 2 * x / i; s = s + a; } Console.WriteLine(" {0: f4} {1: f4}", x, s); Эта последовательность операторов должна быть выполнена в цикле по x. double s, a, x; double xh = 0.1, xk = 1.0001, h = 0.05; int n = (int)((xk - xh) / h + 1); x = xh; for (int j = 1; j < = n; j++) { s = 1; a = 1; for (int i = 1; i < = 12; i++) { a = a * 2 * x / i; s = s + a; } Console.WriteLine(" {0: f4} {1: f4}", x, s); x = x + h; } Console.ReadKey(); Такая структура программы, когда цикл выполняется внутри другого цикла, называется вложенными циклами. Далее приводится результат выполнения программы.
Замечание. Здесь в операторе вывода строка формата содержит пробелы, что и обеспечивает разделение при выводе столбцов значений x и s. Пример 2.14. Вычислить сумму
для значений х, изменяющихся в пределах от 0.2 до 1 с шагом 0.2. Суммирование прекращать, когда очередной член суммы по абсолютной величине станет меньше e = 0.0001. Задача сводится к организации вложенных циклов. Внешний цикл по счетчику обеспечивает изменение х (см. Пример 2.13). Во внутреннем цикле по условию осуществляется вычисление суммы (см. Пример 2.9). Член суммы ai имеет более сложный вид, чем в примере 2.9. Его целесообразно представить в виде двух сомножителей: ai = ci( 2 i – 1 ), где
будем вычислять по рекуррентной формуле, выражая последующий член через предыдущий:
Число значений х на отрезке от 0.2 до 1 с шагом 0.2 равно 5. В программе для контроля при каждом значении х вычисляется также функция const double xh = 0.2, h = 0.2, eps = 0.0001; double a, x, s, y, c; int n = 5, i; x = xh; for (int j = 1; j < = n; j++) { s = 1; c = -1; i = 1; do { c = -c * x * x / ((2 * i - 1) * 2 * i); a = c * (2 * i - 1); s = s + a; i = i + 1; } while (Math.Abs(a) > = eps); y = Math.Cos(x) + x * Math.Sin(x); Console.WriteLine(" x= {0: f4} s= {1: f4} y= {2: f4}", x, s, y); x = x + h; } Console. ReadKey();
Вопросы для самопроверки 1. Что такое цикл? Операторы цикла for, while, do … while. Различия между ними. 2. Какие данные необходимы для организации цикла for? Что такое управляющая переменная цикла? 3. Циклы по условию и их организация. 4. Операторы break и continue. В каких случаях они используются? 5. Типовые алгоритмы циклической структуры: вычисление суммы n слагаемых, вычисление произведения n сомножителей, вычисление факториала, табулирование функции. 6. Вычисление суммы с использованием рекуррентных соотношений. 7. Вложенные циклы. 8. Согласование (приведение) типов. 9. Вывод с использованием формата.
|




 .
.
 при изменении x в пределах от xh = -2.5 до xk = 2.5 с шагом h = 0.5.
при изменении x в пределах от xh = -2.5 до xk = 2.5 с шагом h = 0.5.
 использован метод Pow класса Math.
использован метод Pow класса Math.
 ,
,
 при x = 0.5. Суммирование прекратить, когда очередной член суммы будет меньше заданного ε = 0.0001.
при x = 0.5. Суммирование прекратить, когда очередной член суммы будет меньше заданного ε = 0.0001.
 на отрезке [-1, 0.3] с точностью ε = 0.0001, принимая за начальное приближение x 0 = -0.4 и вычисляя последовательно
на отрезке [-1, 0.3] с точностью ε = 0.0001, принимая за начальное приближение x 0 = -0.4 и вычисляя последовательно  , i = 1, 2, 3, …, пока не будет выполнено условие
, i = 1, 2, 3, …, пока не будет выполнено условие  .
. не выполняется, то следует переслать значение х1 в переменную х0 (х0=х1) и получить в х1 следующее приближение.
не выполняется, то следует переслать значение х1 в переменную х0 (х0=х1) и получить в х1 следующее приближение.
 . Будем последовательно вычитать t из r и подсчитывать количество вычитаний в переменной p. Значение q — результат последнего вычитания, когда в первый раз будет выполнено условие
. Будем последовательно вычитать t из r и подсчитывать количество вычитаний в переменной p. Значение q — результат последнего вычитания, когда в первый раз будет выполнено условие 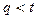 .
.

 при x, изменяющемся в пределах от 0.1 до 1 с шагом 0.05.
при x, изменяющемся в пределах от 0.1 до 1 с шагом 0.05.
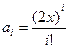
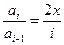




 , которая приближенно может быть представлена в виде указанной суммы.
, которая приближенно может быть представлена в виде указанной суммы.



