Если твердое тело вращается вокруг закрепленной оси z и известна зависимость угла поворота  , то можно рассчитать проекции на ось вращения его угловой скорости
, то можно рассчитать проекции на ось вращения его угловой скорости  и углового ускорения
и углового ускорения  .
.
Если известна зависимость  и начальные условия
и начальные условия 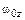 и
и  , то можно найти
, то можно найти  и
и  (обратная задача).
(обратная задача).
5-1. Диск радиуса  м начал вращаться вокруг своей оси без начальной скорости с угловым ускорением, зависящим от времени по закону
м начал вращаться вокруг своей оси без начальной скорости с угловым ускорением, зависящим от времени по закону  . На какой угол (в радианах) он повернется за время
. На какой угол (в радианах) он повернется за время  с, если А = 1 с–2.
с, если А = 1 с–2.
5-2. Диск радиуса  м вращался вокруг своей оси с угловой скоростью
м вращался вокруг своей оси с угловой скоростью  . В момент времени
. В момент времени 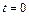 его угловое ускорение стало возрастать по закону
его угловое ускорение стало возрастать по закону  . Какую угловую скорость будет иметь диск через время
. Какую угловую скорость будет иметь диск через время  с, если А = 1 с–2,
с, если А = 1 с–2,  с–1.
с–1.
5-3. Диск радиуса  м вращался вокруг своей оси с угловой скоростью
м вращался вокруг своей оси с угловой скоростью  . В момент времени
. В момент времени 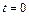 он начал тормозить. Модуль его углового ускорения при этом зависел от времени по закону
он начал тормозить. Модуль его углового ускорения при этом зависел от времени по закону  , А = 5 с–2. Через сколько секунд диск остановится, если
, А = 5 с–2. Через сколько секунд диск остановится, если 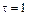 с,
с,  с–1?
с–1?
5-4. Диск радиуса  м начал вращаться вокруг своей оси так, что угол его поворота зависит от времени по закону
м начал вращаться вокруг своей оси так, что угол его поворота зависит от времени по закону  . Через сколько секунд диск остановится, если
. Через сколько секунд диск остановится, если 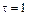 с? А = 1 рад, В = 1 рад.
с? А = 1 рад, В = 1 рад.
5-5. Диск радиуса  м вращался вокруг своей оси с угловой скоростью
м вращался вокруг своей оси с угловой скоростью  . В момент времени
. В момент времени 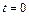 его угловое ускорение стало возрастать по закону
его угловое ускорение стало возрастать по закону  . Через сколько секунд диск будет иметь максимальную угловую скорость, если
. Через сколько секунд диск будет иметь максимальную угловую скорость, если 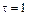 с, А = B = c–2,
с, А = B = c–2,  с–1.
с–1.
 5-6. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком (см. рис.). Найти угол поворота (в радианах) диска за
5-6. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком (см. рис.). Найти угол поворота (в радианах) диска за  с, если
с, если  с–1.
с–1.
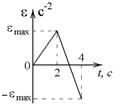
5-7. Диск вращается с нулевой начальной скоростью и с угловым ускорением, зависимость от времени которого задается графиком. Найти максимальную угловую скорость диска в интервале времени 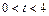 с, если
с, если 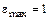 с–2.
с–2.
 5-8. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком.
5-8. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком.
Найти максимальный угол поворота диска (в радианах) в интервале времени от t = 0 до  с, если
с, если  с–1.
с–1.
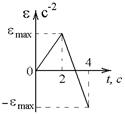
5-9. Диск вращается с угловым ускорением, зависимость от времени которого задается графиком. Найти угловую скорость диска в момент времени  с, если
с, если 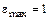 с–2.
с–2.
5-10. Частица движется вдоль окружности с радиусом 1 м в соответствии с уравнением  , где
, где  угол в радианах,
угол в радианах,  время в секундах. Определить момент времени, когда величина нормального ускорения частицы равна нулю.
время в секундах. Определить момент времени, когда величина нормального ускорения частицы равна нулю.

 , то можно рассчитать проекции на ось вращения его угловой скорости
, то можно рассчитать проекции на ось вращения его угловой скорости  и углового ускорения
и углового ускорения  .
. и начальные условия
и начальные условия 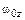 и
и  , то можно найти
, то можно найти  и
и  (обратная задача).
(обратная задача). м начал вращаться вокруг своей оси без начальной скорости с угловым ускорением, зависящим от времени по закону
м начал вращаться вокруг своей оси без начальной скорости с угловым ускорением, зависящим от времени по закону  . На какой угол (в радианах) он повернется за время
. На какой угол (в радианах) он повернется за время  с, если А = 1 с–2.
с, если А = 1 с–2. . В момент времени
. В момент времени 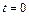 его угловое ускорение стало возрастать по закону
его угловое ускорение стало возрастать по закону  . Какую угловую скорость будет иметь диск через время
. Какую угловую скорость будет иметь диск через время  с–1.
с–1. , А = 5 с–2. Через сколько секунд диск остановится, если
, А = 5 с–2. Через сколько секунд диск остановится, если 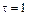 с,
с,  . Через сколько секунд диск остановится, если
. Через сколько секунд диск остановится, если  . Через сколько секунд диск будет иметь максимальную угловую скорость, если
. Через сколько секунд диск будет иметь максимальную угловую скорость, если  5-6. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком (см. рис.). Найти угол поворота (в радианах) диска за
5-6. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком (см. рис.). Найти угол поворота (в радианах) диска за  с, если
с, если  с–1.
с–1.
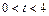 с, если
с, если 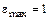 с–2.
с–2. 5-8. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком.
5-8. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком.
 , где
, где  угол в радианах,
угол в радианах,  время в секундах. Определить момент времени, когда величина нормального ускорения частицы равна нулю.
время в секундах. Определить момент времени, когда величина нормального ускорения частицы равна нулю.


