Швидке перетворення Фур'є
Знаходження спектральних складових З цієї причини представляють значний інтерес обчислювальні процедури, які зменшують кількість множень і складань. Основний принцип усіх цих алгоритмів полягає в розкладанні операцій обчислення ДПФ сигналу довжини При реалізації ШПФ можливі декілька варіантів організації обчислень залежно від способу ділення послідовності відліків на частини (проріджування за часом або по частоті) і від того, на скільки фрагментів розбивається послідовність на кожному кроці (основа ШПФ). Найбільш простими і широко використовуваними є алгоритми ШПФ з основою 2, коли довжина послідовності Проаналізуємо більш детально операції ДПФ на прикладі N =8. У цьому випадку, ввівши загальноприйняте в літературі позначення для дискретних експоненціальних функцій
матимемо Користуючись матричним представленням вираз для обчислення ДПФ (вже без множника 1 /N)
може бути представлений у вигляді добутку
де матриця ДПФ прийме вигляд
і вектор Проаналізуємо
Рисунок 7.1 – Комплексна площина Показані числа
Суми виду (7.18) називають згортками. Згортки, які мають вказану властивість називають круговими. Звернемо також увагу на те, що числа, які відповідають точкам розташованим діаметрально протилежно на колі відрізняються лише знаком. Тому
В кожній строчці цієї матриці можна побачити або однакові або такі, що різняться за знаком члени. Ідея ШПФ застосовує описані вище властивості кругової згортки і, крім того, передбачає скорочення кількості операцій множення відповідно до тотожності
Ліворуч у виразі (7.22) два множення, а праворуч лише одне. З урахуванням цього знайдемо складові дискретного спектру:
Видно, що у круглих дужках маються лінійні комбінації елементів вектора Ці три послідовні етапи обчислення можуть бути представлені у вигляді добутку трьох порівняно простих матриць (відповідно з права на ліво). Таким чином, матриця ДПФ приймає вигляд
де
Якщо обчислити добуток цих трьох матриць отримаємо матрицю Процедуру обчислення дискретного спектру зручно подати у вигляді графа (рис. 7.2), який пояснює послідовність дій, виконуваних факторизованою матрицею.
Рисунок 7.2 – Граф ШПФ. Кружком позначено підсумовування, а квадратом - множення на величину, що вказана в квадраті.
Промисловість серійно випускає інтегральні мікросхеми, які виконують чотирьохточкове ДПФ, яке є базовою операцією. Цю мікросхему називають «метеликом». Вона дозволяє виготовляти спеціалізовані процесори ШПФ для сигналів з довільним N. Алгоритмічна схема «метелика» і її позначення наведені на рис. 7.3. Якщо на її вхід поступають комплексні числа
Рисунок 7.3 – Алгоритмічна схема і умовне позначення «метелика»
Як видно зі структурної схеми восьмиточечного спецпроцесора ШПФ реалізованого на «метеликах» (рис. 7.4), в ній реалізовані операції предписані факторизованою матрицею (7.24).
Рисунок 7.4 – Структурна схема спецпроцесора ШПФ на «метеликах»
Формально ШПФ здійснюється шляхом розбивання вихідної послідовності на парні Далі алгоритм обчислення відповідає рис. 7.4. Видно, що вся операція складається з трьох етапів. В загальному випадку для N -точкового ШПФ потрібно
|

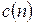 дискретного комплексного сигналу
дискретного комплексного сигналу  безпосередньо по формулі ДПФ вимагає
безпосередньо по формулі ДПФ вимагає  комплексних множень і
комплексних множень і  комплексних додавань. Оскільки кількість обчислень, а отже, і час обчислень приблизно пропорційні
комплексних додавань. Оскільки кількість обчислень, а отже, і час обчислень приблизно пропорційні  кількість арифметичних операцій дуже велика. Тому знаходження спектру в реальному часі навіть для сучасної обчислювальної техніки є складним завданням.
кількість арифметичних операцій дуже велика. Тому знаходження спектру в реальному часі навіть для сучасної обчислювальної техніки є складним завданням. , де
, де  ціле число.
ціле число. , (7.17)
, (7.17) , тут і далі індекс N =8 опущено для простоти запису.
, тут і далі індекс N =8 опущено для простоти запису. , (7.18)
, (7.18) , (7.19)
, (7.19) , (7.20)
, (7.20) ,
,  - знак транспонування.
- знак транспонування. . Точки
. Точки 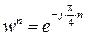 знаходяться на колі одиничного радіусу і являють собою періодичну послідовність. Тобто значення
знаходяться на колі одиничного радіусу і являють собою періодичну послідовність. Тобто значення  повністю визначають будь-яку степінь при
повністю визначають будь-яку степінь при  (за умови N =8).
(за умови N =8).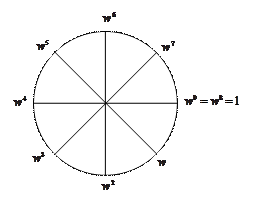
 .
. =
=  .
.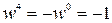 ,
,  ,
,  ,
, 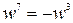 . Тобто будь-яка ціла степінь
. Тобто будь-яка ціла степінь 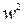 ,
,  . З урахуванням цього матрицю ДПФ можна подати у вигляді
. З урахуванням цього матрицю ДПФ можна подати у вигляді . (7.21)
. (7.21) . (7.22)
. (7.22) ;
;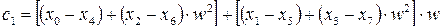 ;
;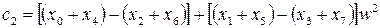 ;
;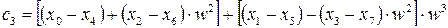 ; (7.23)
; (7.23) ;
; ;
; ;
;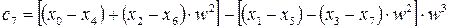 .
. . Кількість таких комбінацій дорівнює 8. В квадратних дужках вагові комбінації сум у круглих дужках (їх теж вісім). Останні операції передбачають утворення вагових сум з результатів у квадратних дужках.
. Кількість таких комбінацій дорівнює 8. В квадратних дужках вагові комбінації сум у круглих дужках (їх теж вісім). Останні операції передбачають утворення вагових сум з результатів у квадратних дужках. , (7.24)
, (7.24) , (7.25)
, (7.25) , (7.26)
, (7.26) . (7.26)
. (7.26) . Розкладання матриць на прості множники виду (7.24) називають факторизацією.
. Розкладання матриць на прості множники виду (7.24) називають факторизацією.

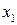 і
і  , тоді на на виході формуються числа згідно з виразами x 1 + x 2 w n і x 1 - x 2 w n. Оскільки комплексні величини являють собою пару чисел (реальні і мнимі частини), тому практично «метелик» має чотири входи і чотири виходи.
, тоді на на виході формуються числа згідно з виразами x 1 + x 2 w n і x 1 - x 2 w n. Оскільки комплексні величини являють собою пару чисел (реальні і мнимі частини), тому практично «метелик» має чотири входи і чотири виходи.
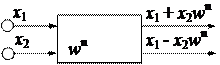

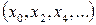 і непарні
і непарні  підпослідовності. З ними далі подібним же чином. Ці процедури повторюються доти, поки не залишиться по одній парі чисел, які поступають на «метелики» першого етапу. Стосовно до восьми точкового ШПФ цими парами є
підпослідовності. З ними далі подібним же чином. Ці процедури повторюються доти, поки не залишиться по одній парі чисел, які поступають на «метелики» першого етапу. Стосовно до восьми точкового ШПФ цими парами є  ,
, 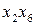 ,
,  ,
,  . На першому етапі операцій множення практично не проводиться (множення на
. На першому етапі операцій множення практично не проводиться (множення на 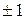 ). Тут формуються суми і різниці отриманих пар.
). Тут формуються суми і різниці отриманих пар.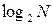 етапів. На кожному з них виконується N /2 операцій множення. Таким чином, алгоритм ШПФ потребує
етапів. На кожному з них виконується N /2 операцій множення. Таким чином, алгоритм ШПФ потребує  операцій множення. Загальний алгоритм ДПФ має
операцій множення. Загальний алгоритм ДПФ має  операцій множення. Тому алгоритм ШПФ порівняно з алгоритмом ДПФ дає виграш по кількості операцій множення в
операцій множення. Тому алгоритм ШПФ порівняно з алгоритмом ДПФ дає виграш по кількості операцій множення в 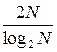 разів.
разів.


