Моделі дискретних сигналів. Дискретизація періодичних сигналів. Дискретне перетворення Фур'є
Дискретне перетворення Фур'є (ДПФ) відноситься до класу основних перетворень при цифровій обробці сигналів. Дискретне перетворення Фур'є, яке частіш за все обчислюється швидкими методами, лежить в основі різних технологій спектрального аналізу. При дискретизації аналогового сигналу його спектр стає періодичним з періодом повторення, рівним частоті дискретизації Розглянемо як початкові дані послідовність
Продовжимо подумки цей сигнал з періодом
Коефіцієнти
Якщо перейти до нової змінної t’ = t / T, отримаємо
Оскільки
Співвідношення (7.5), що дозволяє обчислити комплексні амплітуди гармонік дискретного сигналу, є лінійною комбінацією відліків цього сигналу. Його називають прямимдискретним перетворенням Фур'є (ДПФ). Разом з прямим ДПФ існує і обернене (обернене) дискретне перетворення Фур'є
Зауваження. У розміщенні множника Ортогональний дискретний базис Фур'є, в якому виконується ДПФ, є системою дискретних експоненціальних функцій (ДЕФ), заданою на дискретній часовій осі N відліками,:
Система функцій (7.7) є набором N експонент з частотами, кратними основній частоті Властивості дискретного перетворення Фур'є. 1. Лінійність. Дискретне перетворення Фур'є - лінійне перетворення, тобто якщо послідовностям 2. Симетрія. Властивість симетрії, якою володіє спектр безперервного сигналу, зберігається і для спектру дискретного періодичного сигналу. Якщо відліки
З формули (7.8) виходить, що спектр є спряжено симетричним відносно Гармоніка з нульовим номером (постійна складова), як випливає з (7.5), є середнім значенням усіх відліків сигналу на одному періоді
Якщо
І амплітуда гармоніки з номером 3. ДПФ кругової згортки. Візьмемо дві послідовності
Знайдемо
При виведенні формули (7.12) врахована властивість зсуву періодичної послідовності. Таким чином, круговій згортці дискретизованих сигналів заданих на одному часовому проміжку відповідає перемножування їх спектрів. Обчислення кругової згортки двох сигналів за допомогою ДПФ здійснюється за наступним алгоритмом: · обчислення ДПФ вихідних сигналів за формулою (7.5); · перемножування коефіцієнтів отриманих ДПФ згідно (7.12); · обчислення сигналу 4. Рівність Парсеваля для дискретних сигналів. Визначимо значення
При виведенні формули (7.13) використана умова ортогональності дискретних експоненціальних функцій
Таким чином, потужність сигналу 5. Зв'язок ДПФ і спектру дискретного сигналу. Маючи один і той же набір значень дискретного сигналу
Із співвідношення (7.15) маємо важливий висновок: якщо додати до кінцевого набору відліків деяку кількість нулів, спектральна функція дискретного сигналу, природно, не зміниться, але ДПФ дасть більше число спектральних відліків, які відповідатимуть частотам більш щільно розташованим в інтервалі від нуля до частоти дискретизації. 6. Обчислення оберненого ДПФ за допомогою прямого ДПФ. Для обчислення оберненого ФПФ можна без будь-яких змін застосовувати пряме ДПФ. Обернене ДПФ N -точкової послідовності
Права частина цього виразу є ДПФ послідовності
Далі будемо користуватися більш поширеним представленням прямого та оберненого перетворення Фур'є, коли множник 1/N застосовується у співвідношенні для обчислення оберненого перетворення Фур'є.
|

 . З іншого боку, дискретному спектру повинен відповідати періодичний сигнал.
. З іншого боку, дискретному спектру повинен відповідати періодичний сигнал. дискретних відліків
дискретних відліків  , заданих на відрізку
, заданих на відрізку  ,
, 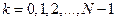 . Моделлю послідовності таких відліків є сигнал із зміщених за часом дельта-функцій:
. Моделлю послідовності таких відліків є сигнал із зміщених за часом дельта-функцій: . (7.1)
. (7.1) . Оскільки дискретний сигнал (7.1) - періодичний, його спектр має бути дискретним з відстанню між гармоніками, рівними
. Оскільки дискретний сигнал (7.1) - періодичний, його спектр має бути дискретним з відстанню між гармоніками, рівними  . Цей дискретний періодичний сигнал можна представити рядом Фур'є
. Цей дискретний періодичний сигнал можна представити рядом Фур'є . (7.2)
. (7.2) цього ряду знаходять згідно з формулою
цього ряду знаходять згідно з формулою (7.3)
(7.3) . (7.4)
. (7.4) , остаточно маємо
, остаточно маємо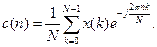 (7.5)
(7.5)
 (7.6)
(7.6)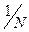 у виразі (7.5) немає повної єдності. У деяких джерелах цей множник відносять до формули оберненого (оберненого) ДПФ, видаляючи його з формули для прямого ДПФ.
у виразі (7.5) немає повної єдності. У деяких джерелах цей множник відносять до формули оберненого (оберненого) ДПФ, видаляючи його з формули для прямого ДПФ. (7.7)
(7.7)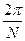 , оскільки
, оскільки 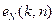 періодична по
періодична по  з періодом
з періодом  з одним і тим же періодом
з одним і тим же періодом  і
і  , то послідовності
, то послідовності  відповідатиме спектр
відповідатиме спектр  .
. , утворюють спряжені пари:
, утворюють спряжені пари: . (7.8)
. (7.8) відповідають від’ємним частотам. При вивченні амплітудного спектру сигналу вони не дають нової інформації.
відповідають від’ємним частотам. При вивченні амплітудного спектру сигналу вони не дають нової інформації. . (7.9)
. (7.9)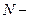 парне число, тоді
парне число, тоді (7.10)
(7.10) .
. і
і  однакової довжини
однакової довжини  . (7.11)
. (7.11) (7.12)
(7.12) за допомогою оберненого ДПФ отриманої послідовності
за допомогою оберненого ДПФ отриманої послідовності  .
. , використовуючи формулу ДПФ
, використовуючи формулу ДПФ
 (7.13)
(7.13) . (7.14)
. (7.14) цього дискретного сигналу по формулі
цього дискретного сигналу по формулі  , або його ДПФ по формулі (7.5). Порівняння цих формул показує, що ДПФ є просто дискретними відліками спектральної функції дискретного сигналу, які відповідають частотам
, або його ДПФ по формулі (7.5). Порівняння цих формул показує, що ДПФ є просто дискретними відліками спектральної функції дискретного сигналу, які відповідають частотам  :
: . (7.15)
. (7.15) , визначається наступним чином
, визначається наступним чином  . (7.16)
. (7.16) , яке може бути обчислене з використанням одного з алгоритмів обчислення прямого ДПФ (наприклад, одного з ШПФ). Шукану послідовність
, яке може бути обчислене з використанням одного з алгоритмів обчислення прямого ДПФ (наприклад, одного з ШПФ). Шукану послідовність  можна отримати, взявши комплексно спряжений з (7.16) вираз і помножити його на N, а саме
можна отримати, взявши комплексно спряжений з (7.16) вираз і помножити його на N, а саме .
.


