Z-перетворення
Зручним способом аналізу дискретних послідовностей є Z -перетворення. При Z -перетворенні різницеві рівняння, що описують роботу дискретної системи, перетворюються в рівняння алгебраїчні, з якими простіше виконувати необхідні дії. Z -перетворення відіграє для дискретних сигналів і систем таку ж роль, як перетворення Лапласа - для аналогових сигналів. Визначення Z -преобразования. Дискретній послідовності відліків
Функція Отримаємо Z -перетворення для деяких дискретних сигналів, що часто зустрічаються на практиці. Одиничний імпульс, який визначається як
Використовуючи формулу (7.27), отримаємо:
Функція Одиничний стрибок, який визначається як
Використовуючи визначення Z -перетворення, отримуємо
Ряд (7.31) є сумою нескінченної геометричної прогресії з першим членом 1 і знаменником
Значення Експоненціальна дискретна функція
Як і у попередньому випадку, цей ряд є сумою геометричної прогресії з першим членом, рівним 1 і знаменником
Комплексна дискретна експонента, яка визначена співідношенням
причому Зв'язок Z –перетворенняз перетворенням Лапласа знайдемо, записавши аналоговий сигнал у вигляді суми дискретних відліків і набору дельта-функцій
де
Скориставшись фільтрувальною властивістю дельта-функції, отримаємо
Порівнюючи співвідношення (7.27) і (7.40), помічаємо, що одна формула переходить в іншу при заміні
Сенс використання Z -преобразования при аналізі дискретних сигналів витікає з наступного. Оскільки справедливе співвідношення
тоді зміна фазової характеристики сигналу Перехід від перетворення Лапласа до Z -перетворення при описанні дискретних систем потрібний з наступної причини. Дискретизація аналогового сигналу призводить до періодичності частотного спектру, тобто появи нескінченного ряду зсунутих копій спектру початкового безперервного сигналу. Очевидно, ефект дискретизації призводить до появи в площині При переході від Таким чином, взаємна відповідність між Z -перетворенням
Подібними формулами описується зв’язок Z -перетворення
Зв'язок ДПФ з Z -перетворенням. Порівнюючи формулу прямого ДПФ дискретної послідовності Отримаємо Z -перетворення послідовності через коефіцієнти ДПФ цієї послідовності
Формула (7.43) показує, що Z -перетворення кінцевої послідовності Властивості Z -перетворення 1. Лінійність. Якщо 2. Затримка (зсув послідовності). Якщо Z -перетворення сигналу Доведення.
Таким чином, при затримці сигналу на Зокрема, якщо сигнал
3. Згортка. Введемо дискретну лінійну згортку
Обчислимо її Z -перетворення:
Отже, Z -перетворення лінійної згортки двох дискретних сигналів дорівнює добутку їх Z -перетворень. Системна функція (передавальна функція) дискретного фільтру. Застосуємо третю властивість Z -перетворення до рівняння дискретної фільтрації:
де
Враховуючи, що Застосуємо Z -перетворення до обох частин різницевого рівняння
і звідси отримуємо загальний вигляд передавальної функції:
Таким чином, передавальна (системна) функція дискретної системи, що фізично реалізується, може бути представлена у вигляді відношення поліномів по від’ємних степенях змінної z.
Импульсной характеристикой
где Заметим, что любую дискретную последовательность
Тогда выходной сигнал, исходя из линейности и стационарности рассматриваемой системы, должен представлять собой линейную комбинацию импульсных характеристик:
Выражение (8.3) представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра. Если фильтр физически реализуем (каузален), то его реакция на выходе не может появиться раньше воздействия на его входе (принцип временного детерминизма). Следовательно, его импульсная характеристика должна равняться нулю в отсчетных точках, предшествующих моменту подачи входного импульса, т.е.
Оскільки системна функція є Z -перетворенням від імпульсної характеристики системи Очевидно, щоб отримати частотний коефіцієнт передач (частотну характеристику) дискретної системи з його системної функції, в останній треба зробити підстановку: Таким чином, маючи різницеве рівняння або структурну схему дискретної системи, не складно визначити її системну функцію і частотний коефіцієнт передачі. Приклад. Визначити системну функцію рекурсивного фільтру другого порядку.
Рішення. Введемо для аналізу проміжний сигнал
Застосовуючи Z –перетворення до рівнянь (7.51) і (7.52), отримуємо:
Отже,
і Різницеві рівняння зазвичай визначені при
Для багатьох сигналів властивості одностороннього Z -перетворення аналогічні властивостям звичайного Z -перетворення. Основним виключенням є властивість, пов'язана із зсувом (затримкою) сигналів. Так, затримка на один відлік як і раніше призводить до множення одностороннього Z–перетворення на Обернене Z -перетворення. Відповідно до (7.54) функція
а потім обчислимо інтеграли від обох частин отриманої рівності, взявши за контур інтегрування замкнуту криву, що лежить цілком в області аналітичності і охоплює усі полюси функції
Очевидно, інтеграли від усіх доданків правої частини перетворяться на нуль, за винятком доданку з номером
де Вираз (7.56) називають оберненим Z -перетворенням, воно дозволяє знайти відліки Існує декілька методів обчислення оберненого Z -перетворення. Найчастіше користуються теоремою про вирахування (вычеты), згідно якої інтеграл по замкненому контуру від функції комплексного аргументу з точністю до множника
Обчислення вирахувань пов'язане з представленням функції
де Для знаходження вирахувань використовують наступні формули: · У разі простого (одноразового) полюса, тобто полюсу з
· У разі
Приклад 1. Визначити по зображенню Знайдемо підінтегральний вираз оберненого Z-перетворення:
Функція
Приклад 2. Знайти відліки сигналу Підінтегральний вираз оберненого Z –перетворення дорівнює:
Функція
Другим методом обчислення оберненого Z -перетворення, вживаним на практиці, є метод розкладання функції
де
Приклад 3. Обчислити обернене Z –перетворення функції Представимо
Із зіставлення виду отриманих доданків з прикладами Z -перетворень типових дискретних сигналів (які були розглянуті) видно, що перший доданок відповідає одиничному стрибку з амплітудою, рівною 2, а другий - дискретній показовій функції
|

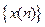 ставиться у відповідність функція комплексної змінної z, яка визначається таким чином,
ставиться у відповідність функція комплексної змінної z, яка визначається таким чином, (7.27)
(7.27) визначена тільки для тих значень z, при яких ряд (7.27) сходиться. Якщо послідовність
визначена тільки для тих значень z, при яких ряд (7.27) сходиться. Якщо послідовність  має обмежену довжину, то
має обмежену довжину, то  .
. . (7.28)
. (7.28) (7.29)
(7.29) сходиться в усій комплексній площині.
сходиться в усій комплексній площині. . (7.30)
. (7.30) (7.31)
(7.31) . Як відомо, такий ряд сходиться при
. Як відомо, такий ряд сходиться при  тобто при
тобто при  і його сума складає
і його сума складає (7.32)
(7.32) є єдиною особливою точкою (полюсом) функції
є єдиною особливою точкою (полюсом) функції  . (7.33)
. (7.33)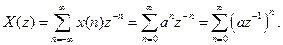 (7.34)
(7.34) . Таким чином, ряд сходиться при
. Таким чином, ряд сходиться при  тобто при
тобто при 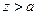 , і має особливу точку при
, і має особливу точку при  :
: (7.35)
(7.35) . (7.36)
. (7.36) (7.37)
(7.37) , оскільки єдиною особливою точкою
, оскільки єдиною особливою точкою  .
.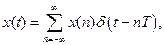 (7.38)
(7.38) крок дискретизації. Перетворення Лапласа для такого сигналу дорівнює
крок дискретизації. Перетворення Лапласа для такого сигналу дорівнює . (7.39)
. (7.39) (7.40)
(7.40) . Таким чином, Z -перетворення можна отримати з перетворення Лапласа шляхом переходу до нової змінної:
. Таким чином, Z -перетворення можна отримати з перетворення Лапласа шляхом переходу до нової змінної: (7.41)
(7.41) , (7.42)
, (7.42) означає затримку сигналу на один крок дискретизації
означає затримку сигналу на один крок дискретизації  і відповідає затримці сигналу на один такт в
і відповідає затримці сигналу на один такт в  області.
області. нескінченної конфігурації особливих точок (полюсів і нулів).
нескінченної конфігурації особливих точок (полюсів і нулів). площини до
площини до  площини точка
площини точка  відображується в точку
відображується в точку  . Тому шлях уздовж уявної осі
. Тому шлях уздовж уявної осі  в
в  і, отже
і, отже  Можна показати, що ліва (стійка) смуга
Можна показати, що ліва (стійка) смуга 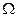 відображується всередину кола одиничного радіусу
відображується всередину кола одиничного радіусу  описується наступним чином:
описується наступним чином: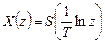 ;
;  .
.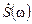 (при цьому немає необхідності вважати послідовність однобічною):
(при цьому немає необхідності вважати послідовність однобічною): ;
;  .
. з формулою Z -перетворення, побачимо, що коефіцієнти ДПФ
з формулою Z -перетворення, побачимо, що коефіцієнти ДПФ  дорівнюють значенням Z -перетворення цього сигналу в
дорівнюють значенням Z -перетворення цього сигналу в  точках, рівномірно розподілених по одиничному колу Z-площини. Ці коефіцієнти однозначно представляють саму послідовність, оскільки вона може бути точно відновлена за допомогою оберненого ДПФ.
точках, рівномірно розподілених по одиничному колу Z-площини. Ці коефіцієнти однозначно представляють саму послідовність, оскільки вона може бути точно відновлена за допомогою оберненого ДПФ. . (7.43)
. (7.43) безпосередньо пов'язано з коефіцієнтами
безпосередньо пов'язано з коефіцієнтами  ,
,  , її ДПФ.
, її ДПФ. і
і  є Z -перетвореннями відповідних сигналів
є Z -перетвореннями відповідних сигналів  і
і  , тоді сигналу
, тоді сигналу  відповідатиме Z -перетворення
відповідатиме Z -перетворення  при будь-яких постійних
при будь-яких постійних  і
і 
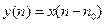 , затриманого на
, затриманого на  тактів, буде рівне
тактів, буде рівне 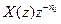 .
. . (7.44)
. (7.44) .
. отриманий шляхом зсуву сигналу
отриманий шляхом зсуву сигналу  . Отже, символ
. Отже, символ  , яку визначимо таким чином:
, яку визначимо таким чином: (7.45)
(7.45) . (7.46)
. (7.46)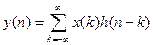 . Оскільки вихідний сигнал дискретної системи є лінійною згорткою вхідного сигналу з імпульсною характеристикою системи, тоді
. Оскільки вихідний сигнал дискретної системи є лінійною згорткою вхідного сигналу з імпульсною характеристикою системи, тоді , (7.47)
, (7.47) - Z -перетворення відповідно вхідного і вихідного сигналів системи, а
- Z -перетворення відповідно вхідного і вихідного сигналів системи, а  – Z -перетворення її імпульсної характеристики
– Z -перетворення її імпульсної характеристики . (7.48)
. (7.48) дорівнює відношенню двох
дорівнює відношенню двох 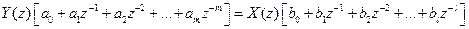 (7.49)
(7.49) (7.50)
(7.50) дискретного фильтра называется его реакция на единичный импульс
дискретного фильтра называется его реакция на единичный импульс  при нулевых начальных условиях:
при нулевых начальных условиях: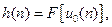 или
или  (1)
(1) оператор преобразования дискретного фильтра. Импульсную характеристику фильтра
оператор преобразования дискретного фильтра. Импульсную характеристику фильтра  обычно представляют совокупностью значений
обычно представляют совокупностью значений 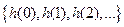 , называемых коэффициентами фильтра.
, называемых коэффициентами фильтра. (2)
(2)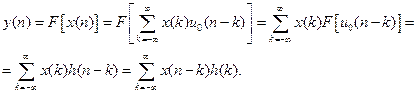 (3)
(3) при
при  . Поэтому верхний предел суммирования в формуле (3) может быть заменен на
. Поэтому верхний предел суммирования в формуле (3) может быть заменен на  :
: (4)
(4) .
. .
.
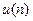 і запишемо рівняння відносно двох суматорів у формі різницевих рівнянь:
і запишемо рівняння відносно двох суматорів у формі різницевих рівнянь: (7.51)
(7.51) (7.52)
(7.52)

 (7.53)
(7.53)
 і мають набір початкових умов. Тому при рішенні практичних задач зазвичай вводять одностороннє Z -перетворення, що має вигляд
і мають набір початкових умов. Тому при рішенні практичних задач зазвичай вводять одностороннє Z -перетворення, що має вигляд . (7.54)
. (7.54) . Помножимо обидві частини ряду (7.54) на множник
. Помножимо обидві частини ряду (7.54) на множник  :
: , (7.55)
, (7.55)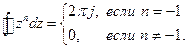
 , (7.56)
, (7.56) - замкнутий контур колом
- замкнутий контур колом  ,
,  - радіус збіжності
- радіус збіжності 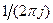 дорівнює сумі вирахувань підінтегральної функції
дорівнює сумі вирахувань підінтегральної функції  в особливих точках (полюсах
в особливих точках (полюсах  ), що охоплюються контуром інтегрування
), що охоплюються контуром інтегрування  . (7.57)
. (7.57)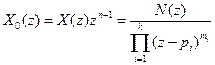 , (7.58)
, (7.58) .
.

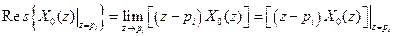 (7.59)
(7.59)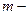 кратного полюса, тобто полюсу
кратного полюса, тобто полюсу  . (7.60)
. (7.60) відліки сигналу
відліки сигналу 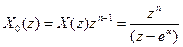 .
. . Відповідно до (7.59) отримуємо:
. Відповідно до (7.59) отримуємо: .
. .
. .
. .
.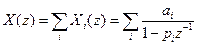 ,
, - Z –перетворення з одним простим полюсом. З урахуванням того, що кожен доданок
- Z –перетворення з одним простим полюсом. З урахуванням того, що кожен доданок  має обернене Z–перетворення виду
має обернене Z–перетворення виду  , отримуємо:
, отримуємо:
 .
. .
. . Отже, шукана послідовність має вигляд:
. Отже, шукана послідовність має вигляд: .
.


