Адиабатический процесс. Уравнение Пуассона
Адиабатическим называется процесс, происходящий в условиях тепловой изоляции системы, когда d Q = 0. Работа, совершаемая системой в адиабатическом процессе, равна взятому с противоположным знаком изменению внутренней энергии d A = - dU. Если адиабатический процесс проводится с идеальным газом, то d A = - CV dT, или A 12 = - CV (T 2 – T 1). Найдем, как связаны между собой параметры состояния идеального газа, совершающего квазистатический адиабатический процесс. Учитывая, что d Q = 0, а dU = CV dT, уравнение первого начала термодинамики (3.3), можно переписать в виде
Пользуясь соотношением (5.4) можно выразить dT через dP и dV
и подставить в (6.1). Принимая во внимание, что CV + R = CP получим
Введем обозначение При этом произойдет разделение переменных Интегрируя, получим Это дает уравнение адиабаты в переменных давление-объем
Соотношение (6.3) называется уравнением Пуассона. Величина g = CP / CV называется показателем адиабаты или адиабатической постоянной. Пользуясь тем, что PV = RT, легко получить уравнение адиабаты в переменных T-V и T-P
Так как CP > CV, то g > 1. Тогда из (6.4) следует, что при адиабатическом сжатии газ нагревается, а при адиабатическом расширении – охлаждается. Это явление используется в дизелях, где воспламенение горючей смеси осуществляется путем адиабатического сжатия. Нагревание объясняется тем, что во время сжатия внешние силы совершают над газом работу, которая идет на увеличение его внутренней энергии, а значит и температуры.
На P-V диаграмме (рис. 6.1) адиабата S-S внешне похожа на изотерму T-T, но имеет больший наклон. Сравним производные (¶ P /¶ V) T и (¶ P /¶ V)ад, определяющие наклон изотермы и адиабаты. Из уравнения изотермы PV = const следует, что P (dV) T + V (dP) T = 0. Отсюда
Беря дифференциал от обеих частей уравнения адиабаты (6.3), получим
Тогда
Следовательно Так как g > 1, из соотношения (6.8) следует, что при адиабатическом изменении объема давление меняется сильнее, чем при изотермическом.
|

 . (6.1)
. (6.1)
 . (6.2)
. (6.2) , и поделим равенство (6.2) на СV× P× V.
, и поделим равенство (6.2) на СV× P× V. .
. , или
, или  .
. . (6.3)
. (6.3)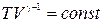 , (6.4)
, (6.4)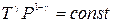 . (6.5)
. (6.5) Рис. 6.1
Рис. 6.1
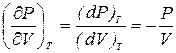 . (6.6)
. (6.6)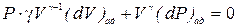 .
. . (6.7)
. (6.7)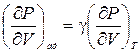 . (6.8)
. (6.8)


