Пробой р-n-перехода
При большом обратном смещении на р-n-переходе, которое создает в нем большое электрическое поле, переход «пробивается» и через него протекает очень большой ток. Существуют три основных механизма пробоя: тепловая неустойчивость, туннельный эффект и лавинное умножение. Первые два механизма мы рассмотрим кратко, а лавинное умножение - более подробно. 1.1 Тепловая неустойчивость Пробой, обусловленный тепловой неустойчивостью, определяет электрическую прочность большинства изоляторов при комнатной температуре, а также является основным фактором в полупроводниках с относительно узкой шириной запрещенной зоны, например, в германии. В р-n-переходе при обратном напряжении протекает обратный ток и, следовательно, выделяется тепло. Увеличение обратного напряжения вызывает повышение температуры перехода. В свою очередь это приводит к возрастанию обратного тока. Количество выделяемого переходом тепла, определяющее его температуру, пропорционально произведению JV. Вследствие теплового нагрева при больших обратных напряжениях возникает участок с отрицательным дифференциальным сопротивлением. На этом участке диод выходит из строя, если не принять специальных мер для ограничения тока (например, включить последовательное сопротивление). Этот эффект называют тепловой неустойчивостью, а напряжение VU - напряжением тепловой неустойчивости. В р-n-переходах со сравнительно большими токами насыщения, например, в германиевых переходах, тепловая неустойчивость становится несущественной по сравнению с другими механизмами пробоя. 1.2 Туннельный эффект Хорошо известно, что квантовомеханическая вероятность прохождения сквозь одномерный прямоугольный потенциальный барьер с высотой Е0 и шириной W определяется выражением
где а Е - энергия частицы. С уменьшением энергии Е вероятность туннеллирования монотонно убывает. При æ W> > 1 она приближенно равна
Аналогичное выражение получается и для р-n-переходов. Плотность туннельного тока определяется выражением
где ε - электрическое поле в переходе, Eg - ширина запрещенной зоны, V - приложенное напряжение, m* - эффективная масса носителя. Когда электрическое поле в Ge или Si достигает 106 В/см, начинают протекать большие токи, обусловленные туннельными переходами между зонами. Чтобы получить такое сильное поле, концентрации примеси в р- и n-областях должны быть достаточно высокими. Доказано, что механизм пробоя в кремниевых и германиевых переходах обязан туннельному эффекту при напряжениях пробоя, меньших 4Eg/g. В переходах с напряжением пробоя, превышающим 6Eg/g, механизм пробоя обусловлен лавинным умножением. При напряжении пробоя, лежащем в интервале 4-6Eg/g, в пробое участвуют оба механизма (лавинный и туннельный). Поскольку ширина запрещенной зона Eg в Ge, Si и GaAs уменьшается с повышением температуры, то напряжение пробоя в этих полупроводниках, связанное с туннельным эффектом, имеет отрицательный температурный коэффициент, т.е. падает с повышением температуры. Это объясняется тем, что при более высоких температурах заданная величина тока при пробое Jt достигается при меньших обратных напряжениях (или полях). 1.3 Лавинноеумножение Лавинное умножение, или ударная ионизация, является наиболее важным механизмом пробоя р-n-перехода. Напряжение лавинного пробоя определяет верхний предел обратного напряжения большинства диодов, коллекторного напряжения биполярных транзисторов, напряжения стока МОП-транзисторов и МОП-транзисторов. Кроме того, механизм ударной ионизации используется в мощных генераторах СВЧ-колебаний, таких, как лавинно-пролетные диоды, и в приемниках оптических сигналов, таких, как лавинные фотодиоды. Найдем сначала основное выражение для условия пробоя. Пусть с левой стороны обедненной области шириной W втекает ток JРО. Если электрическое поле в обедненной области настолько велико, что вследствие ударной ионизации могут генерироваться электронно-дырочные пары, то дырочный ток JР будет нарастать с координатой и на правой границе обедненной области (a=W) достигнет величины МрJPO. Аналогично электронный ток Jn будет возрастать в направлении от х=Wkx=0. Полный ток (J= JP+ Jn) в стационарных условиях постоянен. Приращение дырочного тока в точке с координатой х равно числу электронно-дырочных пар, генерируемых за 1 с на расстоянии dx:
или
коэффициенты ионизации электронов и дырок (apи an) рассмотрены в главе 1. Решение уравнения (21.4) с ограниченным условием J=Jp(W)=MpJpo записывается в виде
где Мр коэффициент умножения дырок, равный
Уравнение (21.5) можно записать в виде
Напряжением лавинного пробоя называется напряжение, при котором Мр стремится к бесконечности. Следовательно, условней пробоя задается интегралом ионизации
Если лавинный процесс инициируется не дырками, а электронами, то интеграл ионизации имеет вид
Уравнения (21.8) и (21.9) эквивалентны, т.е. условия пробоя зависят только от процессов внутри обедненной области, а не от носителей или первоначальных токов, вызвавших лавинный процесс. Ситуация не меняется, если пробой вызван смешанными первичными токами: лишь бы выполнялось одно из условий - (21.8) или (21.9). Для полупроводников с равными коэффициентами ионизации (an=ap=a), например для GaР, интегралы (21.8) и (21.9) принимают вид
Используя полученные условия пробоя и располагая зависимостью коэффициентов ионизации от поля, можно определить напряжение пробоя, максимальное электрическое поле и ширину обедненной области. Электрическое поле и потенциал обедненного слоя находятся из уравнения Пуассона. Положение границ слоя, удовлетворяющее уравнению (21.8), можно определить численно методом последовательных приближений. Если ширина обедненной области известна, то напряжение пробоя VB несимметричного резкого перехода
а для линейного перехода
где NB - концентрация ионизированной примеси в слаболегированной области, ε s - диэлектрическая проницаемость полупроводника, а - градиент концентрации примеси, ε m - максимальное электрическое поле. Расчетные зависимости пробоя от N0 для резких переходов в Ge, Si, GaAs с ориентацией < 100> и в GaP хорошо согласуются с экспериментальными значениями. В p-n-переходе на кремни максимальное поле определяется выражением
где NВ измеряется в см-3. Вследствие сильной зависимости коэффициентов ионизации от поля величина максимального поля очень слабо зависит от NB и a. Поэтому в первом приближении для данного полупроводника можно считать ε m постоянным. Тогда из выражения (21.11-21.12) следует, что для резкого перехода VB~NВ-10, а для линейного VB~a0, 5. Кроме того, как и следовало ожидать, при фиксированных NВ или a напряжение пробоя возрастает с увеличением ширины запрещенной зоны, поскольку при лавинном умножении происходит переход носителей из одной зоны в другую. На основе рассмотренных выше результатов можно получить приближенную универсальную формулу напряжения пробоя резкого перехода, справедливую для всех изученных полупроводников: VB@60(Eg/1, 1)3/2(NB/1016)-3/4 (21.13а) где Eg - ширина запрещенной зоны при комнатной температуре, эВ; NB - концентрация примеси в слаболегированной области, см-3. Аналогичное выражение для линейного перехода имеет вид VB@60(Eg/1, 1)6/5(a/3x1020)-2/5 (21.13б) где a - градиент концентрации примеси, см-4. Для р-n-перехода, полученного диффузионным методом, с линейным распределением примеси на одной стороне и с постоянной концентрацией примеси на другой стороне перехода напряжение пробоя принимает промежуточное значение между напряжениями пробоя ступенчатого и линейного переходов. Для больших значений a и низких значений NB напряжение пробоя диффузионного перехода приближается к напряжениям для резкого перехода; с другой стороны, для малых a и высоких NB напряжение близко к напряжениям для линейного перехода Результаты, получены в предположении достаточно большой толщины полупроводникового слоя, чтобы при пробое мог существовать обедненный слой шириной W. Однако если ширина полупроводникового слоя W меньше Wm, то еще до лавинного пробоя произойдет прокол прибора (т.е. обедненный слой достигнет границы раздела n-n+). При дальнейшем увеличении обратного смещения неизбежно наступит пробой прибора. Максимальное электрическое поле ε m примерно такое же, как и в приборе без прокола. Следовательно, для напряжения пробоя VBT диода с проколом можно написать
Прокол обычно возникает при достаточно низкой концентрации легирующей примеси NB что имеет место в р+ - p - n+- и р+ - V - n+ - диодах (p означает слаболегированный полупроводник р-типа, а V - слаболегированный полупроводник n-типа). Предполагается, что переход сформирован на эпитаксиальной подложке (т.е. на n -подложке выращен эпитаксиальный слой V -типа толщиной W). Для заданной толщины при уменьшении концентрации примеси напряжение пробоя стремится к постоянному значению, соответствующему проколу эпитаксиального слоя. С повышением температуры напряжение пробоя возрастает. Это можно объяснить тем, что горячие носители, проходя через обедненный слой под действием сильного поля, теряют часть своей энергии при столкновении с оптическими фотонами. Средняя длина свободного пробега электронов между электрон-фотонными столкновениями l падает с повышением температуры. Поэтому при постоянном поле носители, проходя заданное расстояние, отдают кристаллической решетке большую часть энергии. Следовательно, для того, чтобы носители набрали энергию, достаточную для генерации электронно-дырочных пар, требуется большая разрядность потенциалов. Из вычислений следует, что при одинаковых профилях легирования относительные изменения VB перехода с температурой в GaAs примерно совпадают с изменениями в Gе, а в GаР - с изменениями в Si. Необходимо обратить внимание на существенное увеличение напряжения пробоя с повышением температуры при относительно низких концентрациях примеси (или малых градиентах концентрации).
В планарных р-n-переходах необходимо учитывать очень сильное влияние кривизны перехода. Поскольку напряженность электрического поля на цилиндрических и/или сферических областях переходе выше, то напряжение пробоя определяется именно этими областями. Потенциал V(r) и электрическое поле ε (r) в цилиндрическом или сферическом переходе можно найти, решая уравнение Пуассона:
где n=1 для цилиндрических переходов и n=2 для сферических. Решая уравнение (81), получим
где ri - радиус кривизны металлургического перехода, а константа должна быть выбрана такой, чтобы удовлетворялись условия пробоя (21.8) или (21.9). Из полученных численными методами результатов следует, что при 300 К для несимметричных резких цилиндрических переходов в кремнии справедливо следующее простое аналитическое выражение:
а для сферических переходов
где VCY и VSP - напряжение пробоя цилиндрического или сферического перехода соответственно, VВ - напряжение пробоя плоскостного перехода, имеющего ту же концентрацию примесей, и h=ri/Wm. Зависимость напряжения пробоя от h для цилиндрического и сферического переходов с линейным распределением примесей, то из результатов вычислений следует сравнительно слабая зависимость напряжения пробоя от радиуса кривизны.
|

 (21.1)
(21.1)
 (21.1a)
(21.1a) (21.2)
(21.2) d(Jp/g)=(Jp/g)(apdx)+ (Jn/g)(andx) (21.3)
d(Jp/g)=(Jp/g)(apdx)+ (Jn/g)(andx) (21.3)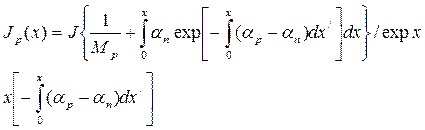 (21.5)
(21.5) (21.6)
(21.6) (21.7)
(21.7) (21.8)
(21.8) (21.9)
(21.9) (21.10)
(21.10) (21.11a)
(21.11a) (21.11б)
(21.11б) (21.12)
(21.12) (21.14)
(21.14)
 (21.15)
(21.15) (21.16)
(21.16) (21.17)
(21.17) (21.18)
(21.18)


