ОБЗОР ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ

 

Разновидностей геометрических образов четыре: точка, линия, поверхность, плоскость. Рассмотрим, как их изображают на ортогональных чертежах.

ТОЧКА. Чтобы спроецировать данную в пространстве точку А, необходимо из нее опустить перпендикуляр на данную горизонтальную плоскость П₁ (рис. 1.4). Точка А₁ будет проекцией точки А и основанием перпендикуляра, опущенного на данную плоскость, а перпендикуляр АА₁ – проецирующим перпендикуляром. Определить положение точки в пространстве одной проекцией невозможно, так как одна и та же проекция может принадлежать нескольким точкам, лежащим на перпендикуляре АА₁. В этом случае говорят, что такой чертеж необратим, то есть по одной проекции нельзя определить, где расположена точка в пространстве.

Положение точки в пространстве будет определено, если её спроецировать на две или три взаимно перпендикулярные плоскости: на горизонтальную П₁, фронтальную П₂ и профильную П₃ (рис. 1.4). Полученные проекции А₁, А₂ и А₃ точки затем совмещают с плоскостью чертежа (например, П₂), что соответствует только одному положению точки в пространстве. Линии чертежа А₁А₂ и А₂А₃ называют линиями проекционной связи или просто линиями связи. Положение любой точки в пространстве определяется расстояниями от плоскостей проекций, что соответствует декартовой прямоугольной системе координат. Координатами называют числа, которые служат для определения положения точки в пространстве. Координату x называют абсциссой, у – ординатой, и z – аппликатой. Абсцисса определяет расстояние точки от плоскости П₃, ордината – от плоскости П₂ и аппликата от плоскости П₁.

Две проекции точки определяют положение её третьей проекции, так как все проекции связаны между собой линиями связи, перпендикулярными соответствующим осям проекций. В дальнейшем удобно пользоваться не трёхпроекционным (рис. 1.5), а двухпроекционным комплексным чертежом (рис. 1.6).

Рис. 1.5

Рис. 1.6

 

ПРЯМАЯ. Этот геометрический образ – одна из разновидностей линии, важнейший и наиболее часто применяющийся как при изображении предметов, условиях различных задач, так и имеющий самостоятельное значение. Проекция прямой – всегда прямая. Наиболее просто прямую представить отрезком, поскольку положение прямой в пространстве определяется положением двух её точек (рис. 1.7, а и б).

 

а) б)

Рис. 1. 7

 

Чтобы положение прямой в пространстве было определённым, необходимо иметь не менее двух проекций отрезка (рис. 1.7б).

Различают прямые общего и частного положений. Прямая общего положения – наклонная ко всем плоскостям проекций, не параллельная и не перпендикулярная ни одной из них. Изображённая на рис. 1.7 прямая – общего положения.

Среди прямых частного положения различают проецирующие прямые и прямые уровня. Первые из них перпендикулярны горизонтальной (рис. 1.8), фронтальной (рис. 1.9) и профильной (рис. 1.10) плоскостям проекций. Вторые – параллельны горизонтальной (рис. 1.11), фронтальной (рис. 1.12) и профильной (рис. 1.13) плоскостям проекций. Уровень прямой – расстояние от прямой до той плоскости проекций, которой она параллельна. Если прямая лежит в той или иной плоскости проекций, одна из проекций такой прямой совпадает с соответствующей осью (X, Y или Z).

 

 

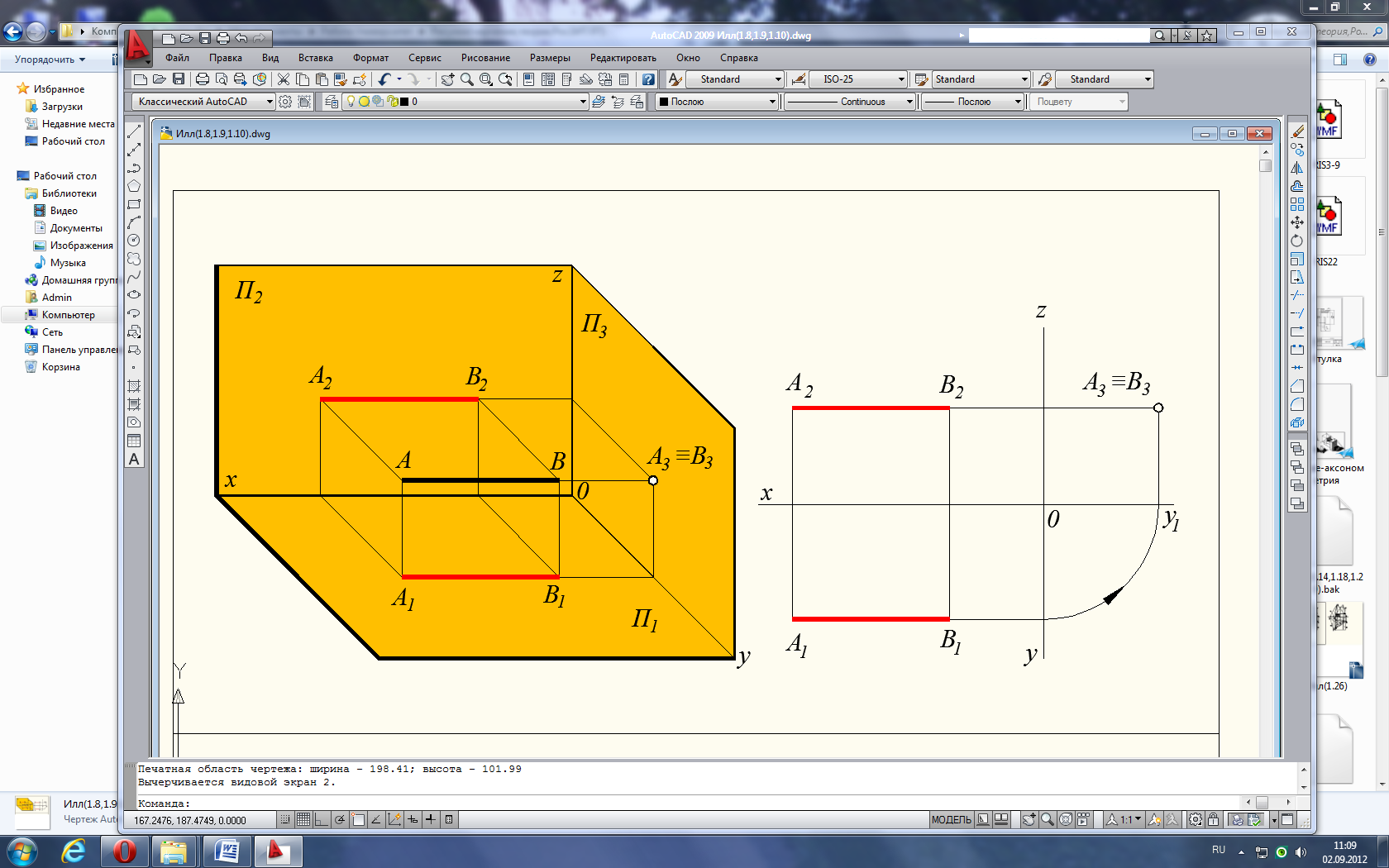
Рис. 1.8

Рис. 1.9

 

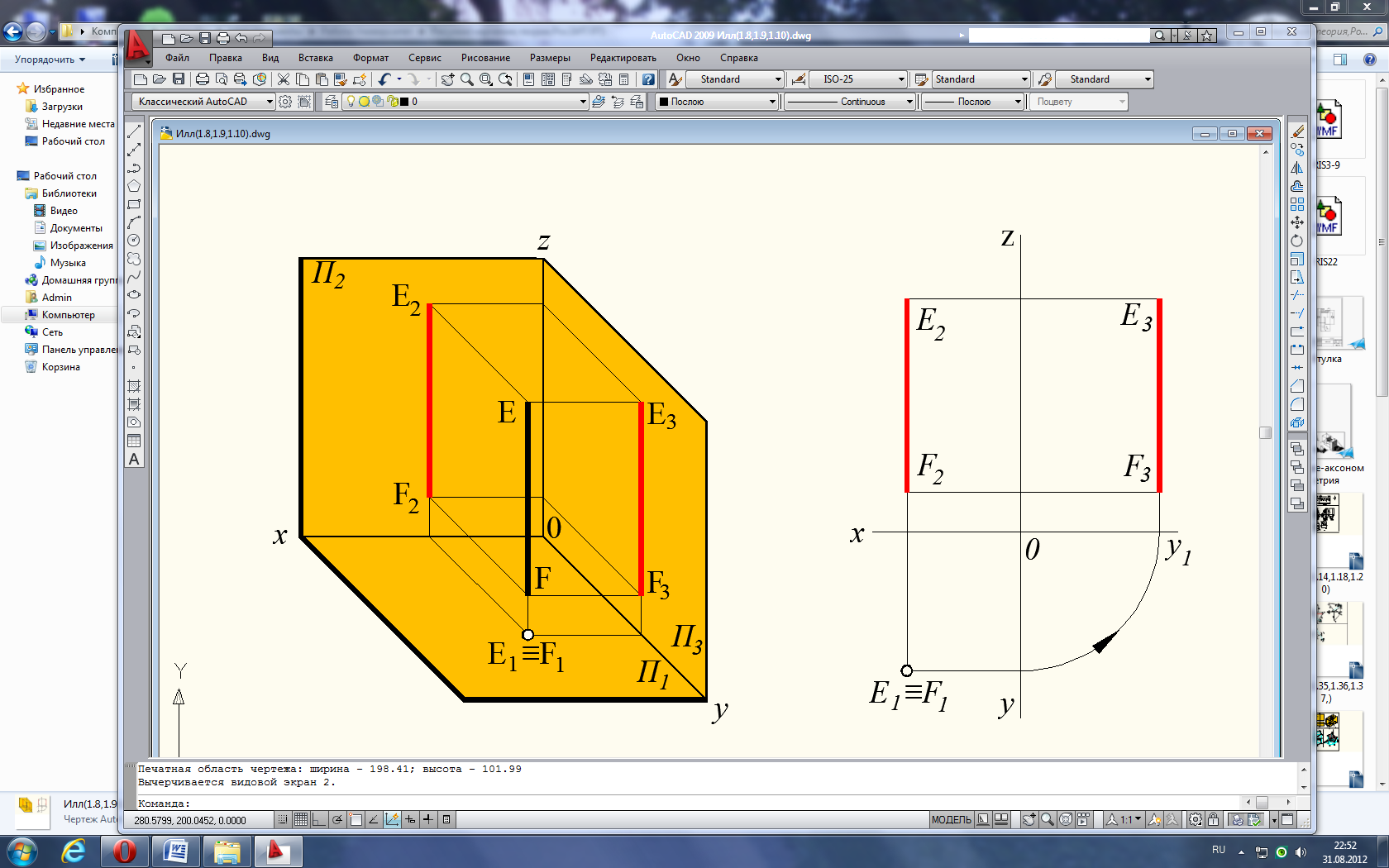
Рис. 1.10

 

Рис. 1.11

 

Рис. 1.12

 

Рис. 1.13

Изображения всех видов прямых на двухпроекционном комплексном чертеже представлены на рис. 1.14.

 

Рис. 1.14

 

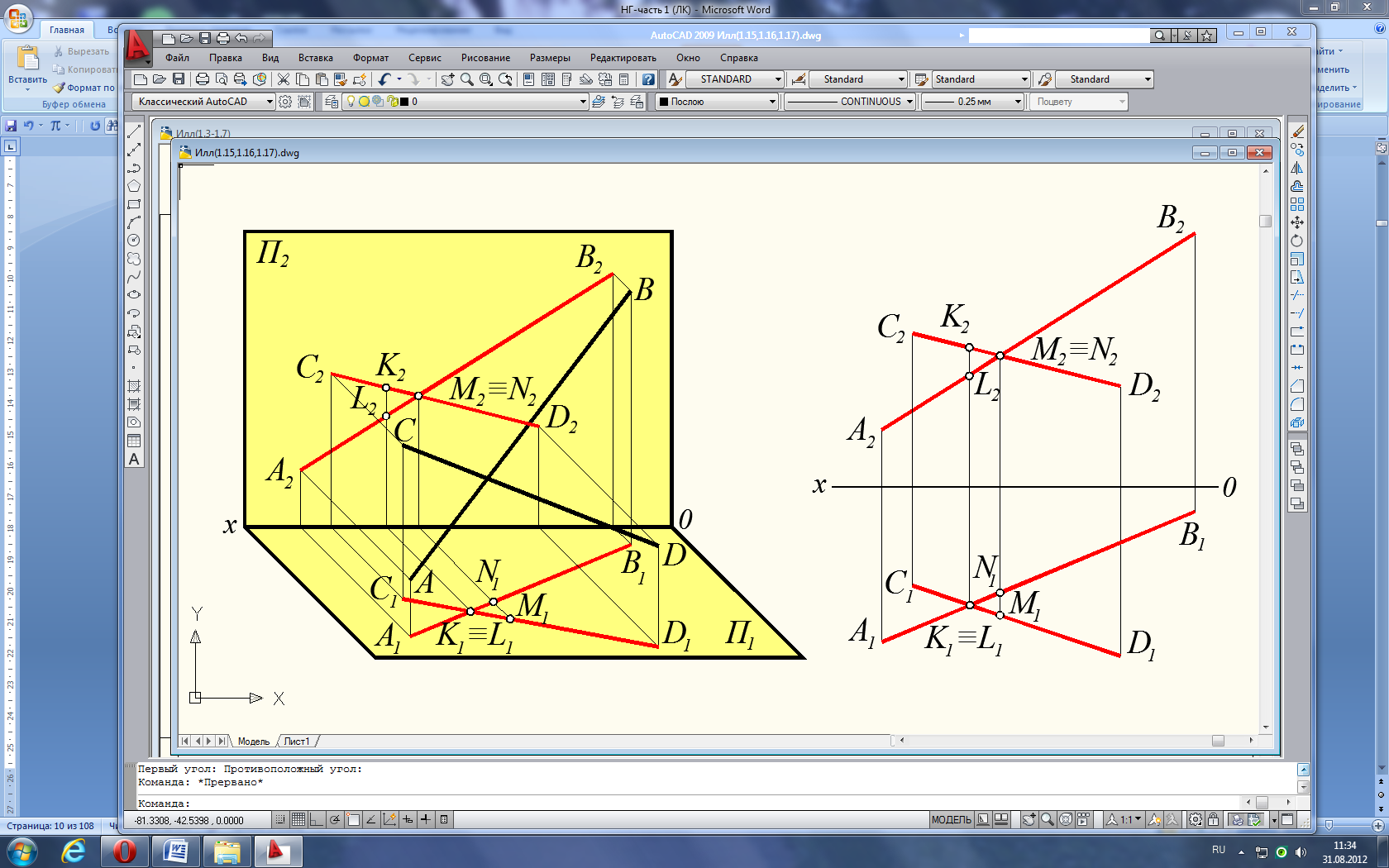
На следующих иллюстрациях представлены изображения трёх случаев взаимного расположения в пространстве двух прямых: прямые параллельны (рис. 1.15), прямые пересекаются (рис. 1.16) и прямые скрещиваются (рис. 1.17).

 

Рис. 1.15

Рис. 1.16

 

 

Рис. 1.17

 

КРИВЫЕ. Любая кривая линия проще всего задаётся своими проекциями. Наибольший интерес представляет изображение окружностей, располагающихся в плоскостях, параллельных горизонтальной (П₁) или фронтальной (П₂) плоскости проекций. На рис. 1.18 представлены двухпроекционные комплексные чертежи для этих случаев расположения окружностей.

ПОВЕРХНОСТЬ. Поверхность – это множество всех последовательных положений движущейся линии, называемой образующей поверхности. Закон перемещения образующей обычно определяется другой линией, называемой направляющей поверхности, а также характером движения образующей по направляющей.

 

Рис. 1.18

 

Образующая, направляющая и характер движения – определитель поверхности, поскольку задать их – тем самым определить поверхность.

Различают поверхности:

– линейчатые (образующая – прямая);

– нелинейчатые (образующая – кривая);

– развёртывающиеся (после разреза по образующей могут быть односторонне совмещены с плоскостью без разрывов и складок);

– неразвёртывающиеся (невозможна процедура развёртывания).

На практике чаще всего встречаются поверхности гранные и поверхности вращения.

Гранные поверхности образовываются при движении прямолинейной образующей по ломаной направляющей. Наиболее часто приходится иметь дело с поверхностями пирамидальной и призматической (рис. 1.19):

Рис. 1.19

Из множества гранных поверхностей выделяют группу многогранников – замкнутых поверхностей, образованных некоторым количеством граней. На рис. 1.20 представлены изображения некоторых наиболее часто встречающихся в практике многогранников.

 

Рис. 1.20

Поверхности вращения образованы вращением некоторой линии (образующей) вокруг некоторой прямой (оси вращения). В общем виде поверхность вращения с возможными принадлежащими ей линиями имеет вид, изображённый на рис. 1.21. Здесь же представлен двухпроекционный чертёж её (определитель поверхности).

 

Рис. 1.21

Изображения некоторых важнейших с точки зрения практического использования тел вращения на двухпроекционном комплексном чертеже представлены на рис. 1.22.

 

 

Рис. 1.22

ПЛОСКОСТЬ. Плоскость можно рассматривать как частный случай поверхности, когда и образующая, и направляющая – прямые, а характер движения образующей – параллельно самой себе. Задать плоскость можно одним из следующих способов:

• тремя точками, не лежащими на одной прямой (рис. 1.23а);

• прямой и не лежащей на ней точкой (рис. 1.23б);

• двумя параллельными прямыми (рис. 1.23в);

• двумя пересекающимися прямыми (рис. 1.23г);

• плоской фигурой (рис. 1.23д);

• следами плоскости (рис. 1.23е).

а) б) в) г) д) е)

Рис. 1.23

След плоскости – прямая, по которой заданная плоскость пересекается с какой-либо плоскостью проекций. Задание плоскости следами равносильно заданию её двумя пересекающимися прямыми: фронталью f₀ и горизонталью h₀ нулевого уровня (в этом случае горизонтальная проекция фронтали и фронтальная проекция горизонтали совпадают с осью Х – f₀₁ ≡ h₀₂).

От одного способа задания плоскости легко перейти к любому другому.

Различают плоскости общего и частного положения.

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций. На чертеже элементы, задающие такую плоскость, в полной мере представлены как на горизонтальной, так и на фронтальной проекциях плоскости (все, изображённые на рис. 1.23 –плоскости общего положения).

Проецирующая плоскость перпендикулярна какой-либо из плоскостей проекций. На чертеже элементы, задающие проецирующую плоскость, вырождаются в прямую на той плоскости проекции, к которой данная плоскость перпендикулярна.

Плоскость уровня параллельна какой-либо плоскости проекций. Любая плоскость уровня – одновременно дважды проецирующая плоскость. Поэтому в случае плоскостей горизонтального или фронтального уровня её вырожденная в прямую проекция параллельна оси Х.

Важнейшие линии плоскости – её фронталь и горизонталь.

Фронталь плоскости – прямая, принадлежащая плоскости и одновременно параллельная фронтальной плоскости проекций. Горизонталь плоскости – прямая, принадлежащая плоскости и одновременно параллельная горизонтальной плоскости проекций. В любой плоскости можно провести бесконечное множество её фронталей и горизонталей.

 

1.2. ГЛАВНАЯ ПРОЕКЦИЯ ГЕОМЕТРИЧЕСКОГО ОБРАЗА.

 

Обзор геометрических образов позволяет сделать некоторые важные выводы.

Любой проецирующий геометрический образ имеет вырожденную проекцию (прямая – вырождается в точку, плоскость – в прямую, поверхность – в своё основание). Эта вырожденная проекция геометрического образа обладает собирательными свойствами: где бы на прямой не лежала принадлежащая ей точка, одна проекция точки совпадает с вырожденной проекцией прямой; где бы в плоскости не лежали принадлежащие ей точка или линия, одна проекция их принадлежит вырожденной проекции плоскости; где бы на поверхности не лежали принадлежащие ей точка или линия, одна проекция их принадлежит вырожденной в основание проекции поверхности или части её.

Наличие у геометрического образа вырожденной проекции является признаком проецирующего геометрического образа и называется егоглавной проекцией. Основное свойство главной проекции геометрического образа – собирательное. Из всего многообразия поверхностей проецирующим геометрическим образом могут быть только прямая призма и прямой цилиндр.