Решение задачи с использованием системы Mathcad

Для построения математической модели в системе Mathcad сформируем начальное выражение критерия оптимизации с использованием жирного знака равенства (комбинация клавиш Ctrl+=).

Далее определим составляющие критерия оптимизации. Для ввода первого выражения выберем пункт меню View (Вид) главного меню Mathcad. В появившемся падающем меню щелкнем по пункту Toolbars (Панели инструментов). Выберем во всплывающем меню пункт Symbolic (Символы). В возникшей панели инструментов Symbolic щелкнем по кнопке с названием Substitute (Подставить). Появится шаблон с метками, вместо которых введем первое выражение, например:

,

воспользовавшись для ввода знака равенства кнопкой с изображением жирного знака равенства на панели инструментов Evalu... (Вычисления) или комбинацией клавиш Ctrl+=. Затем снова щелкнем по кнопке substitute (подставить) на панели Symbolic и введем второе выражение и т.д. до тех пор, пока не разместим все нужные выражения. После этого нажмем клавишу Enter и получим развернутое выражение критерия оптимизации ‑ искомую математическую модель.

Продифференцируем полученное выражение Y относительно искомого параметра S. Во избежание повторной работы выделим выражение с помощью комбинации клавиш Shift+стрелка и скопируем его, нажав Ctrl+Ins. Щелкнем мышью там, где должно быть расположено выражение для дифференцирования, затем по кнопке с изображением знака интеграла и дифференциала на панели инструментов Math (Математика). Появится панель инструментов Calculus (Матанализ). Щелкнем по кнопке d/dx. На рабочем листе возникнет шаблон с двумя метками для ввода искомой переменной и выражения:

.

На месте нижней метки расположим имя искомой переменной (в нашей задаче это S), на месте верхней - развернутое выражение критерия оптимизации Затем вставим знак символического равенства (стрелка вправо) - правый верхний знак на панели инструментов Evalu... - или нажмем комбинацию клавиш Ctrl+. (точка). В заключение воспользуемся кнопкой Enter.

Далее полученное после дифференцирования выражение решим относительно искомого параметра S. Для этого нажатием клавиш (Shift+стрелка влево или вправо) выделим результат дифференцирования или проведем по нему указателем мыши с нажатой левой кнопкой. Скопируем (Ctrl+Ins) результат, укажем щелчком мыши место расположения уравнения и вставим в него скопированную часть (Shift+Ins).

Далее с помощью комбинации клавиш Ctrl+= введем знак булева равенства (жирный знак равно) и число 0. Затем нажмем комбинацию клавиш Ctrl+Shift+точка или щелкнем по правой верхней кнопке (метка и стрелка вправо) на панели инструментов Symbolic. Появится шаблон - метка и стрелка вправо. Вместо метки необходимо ввести ключевое слово solve (решить) и запятую. Появится новая метка, вместо которой следует ввести имя искомой переменной и нажать клавишу Enter. Если все действия были выполнены правильно, появится решение уравнения относительно искомой переменной - выражение для определения оптимального размера поставляемой партии Sopt.

На рис. 4.1.2 представлены результаты решения задачи, когда затраты Cd на доставку партии материалов не зависят от количества сырья в единице поставки, а на рис. 4.1.3 - итоги решения, когда затраты Cd линейно зависят от величины S поставляемой партии материалов:

Cd = Cd + Cdl × S.

Анализируя результаты аналитического решения задачи управления запасами при удовлетворении спроса, когда затраты Cd на доставку партии материалов не зависят от количества сырья в единице поставки (рис. 4.1.2) и когда Cd линейно зависят от величины S поставляемой партии материалов (рис. 4.1.3), мы видим, что конечный результат не изменяется. Квадратное уравнение имеет два решения, из которых выбираем одно - положительное.

Движение запасов при неполном удовлетворении спроса представлено на рис. 4.2.1.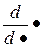