Реология идеальных тел
Рассмотрим простейшие реологические свойства - упругость, пластичность и вязкость трех так называемых идеальных тел. В реологии идеальные тела принято называть именами ученых, которые ввели их впервые [I j: упругое тело называется телом Гука (Нооке, 1635-1703 гг.), пластическое - телом Сен-Венана (St. Venant, 1797-1886 гг.), вязкое - телом Ньютона (I. Newton, 1642-1726 гг.). В качестве моделей идеальных тел обычно используют сталь, пластилин и воду, которые, хотя и обладают всеми реологическими свойствами, как реальные тела, но в большей степени каждому из них присуще одно из свойств: упругость, пластичность или вязкость. Наиболее ярко различие в реологических свойствах этих тел проявляется при сдвиговых деформациях. Это различие может быть лучше всего выражено математически через так называемые реологические модели (реологические уравнения), устанавливающие связь между касательным напряжением (напряжением сдвига) и деформацией сдвига (градиентом сдвига). Реологическая модель упругого тела является выражением закона упругой деформации Гука, сформулированного им в 1678 г., согласно которому касательное напряжение (напряжение сдвига), возникающее при сдвиговой деформации тела, пропорционально деформации сдвига (градиенту сдвига):
где
Реологическая модель пластического тела может быть записана в виде
При малых напряжениях сдвига поведение пластического тела аналогично поведению упругого тела. Однако при достижении некоторого критического значения напряжения сдвига, называемого пределом текучести при сдвиге, пластическое тело потечет. При этом напряжение сдвига будет оставаться приблизительно постоянным, а величина сдвига - безгранично расти. Реологическая модель вязкого тела является выражением закона вязкого трения Ньютона, сформулированного им в 1687 г., согласно которому касательное напряжение (напряжение сдвига), возникающее между соседними слоями жидкости при ее течении, пропорционально поперечному градиенту скорости (скорости сдвига):
где t - напряжение сдвига, Па; μ - динамическая вязкость жидкости, Па*с;
Материалы, поведение которых описывается реологическим уравнением (1.3), называются ньютоновскими жидкостями. Для ньютоновской жидкости единственным реологическим параметром, то есть параметром, характеризующим ее течение, является динамическая вязкость, определяемая из уравнения (1.3) как отношение напряжения сдвига к скорости сдвига. График зависимости напряжения сдвига от меры сдвига (графическое представление реологических уравнений) называется реологической линией (реологической кривой или реограммой). Иногда реологическую линию называют еще кривой консистентности. На рис.1 приведены реологические линии для трех идеальных тел. Стрелки на линиях указывают направление, в котором изменяется напряжение сдвига. Как видно из рис.1.1, если для упругого и вязкого тел линия нагрузки совпадает с линией разгрузки, что свидетельствует о полной обратимости реологического поведения этих тел, то реологическая линия пластического тела имеет упругий участок лишь до предела текучести tт, что свидетельствует об обратимости только той части полной деформации, а те деформации, что были накоплены в процессе течения, являются необратимыми (остаточные деформации).
Рис.1. Реологические линии идеальных тел. а) упругого; б) пластического; в) вязкого
|

 (1.1)
(1.1) - напряжение сдвига, Па;
- напряжение сдвига, Па; - модуль сдвиговой упругости, Па.
- модуль сдвиговой упругости, Па. - градиент сдвига;
- градиент сдвига; (1.2.)
(1.2.)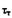 - предел текучести при сдвиге, Па.
- предел текучести при сдвиге, Па. (1.3)
(1.3)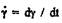 - скорость сдвига
- скорость сдвига





