Аномально-вязкие (неньютоновские) жидкости

Существуют жидкости, кривая течения которых отличается от
представленной на рис. 2. Эти жидкости называются неньютоновски­-
ми. Вязкость неньютоновских жидкостей не остается постоянной при
заданной температуре и давлении и зависит от других факторов таких, как скорость деформации сдвига, конструктивные особенности аппаратуры и предыстории жидкости.

Кривые течения некоторых неньютоновских жидкостей, реологи­ческие характеристики которых не зависят от времени приложения на­грузки, представлены на рис. 3. Такие жидкости называются реостабильными.

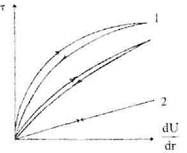
Рис. 3. Кривые течения реостабильных

неньютоновских жидкостей:

1 - вязкопластичная; 2 - псевдопластичная;

3 - дилатантная

Кривая течения 1 принадлежит жидкостям, течение которых во­обще не происходит до достижения некоторого критического напря­жения τ _о, а при τ > τ _о развивается вязкое течение. Реологическое уравне­ние такой жидкости можно представить в виде

 

где τ _о - предельное напряжение сдвига;

μ _о- бингамовская или пластичная вязкость.

Жидкость, подчиняющуюся реологическому закону (4), называют вязкопластичной жидкостью Швелова-Бингама. Если τ < τ _о, она ведет себя как твердое тело, а при τ > τ _о - как ньютоновская жидкость. Вязкопластичные свойства проявляют нефти с большим содержанием парафина, глинистые растворы, краски, шламы, сточные грязи.

В табл. 2 приложения приводятся данные по предельному напря­жению сдвига от температуры для некоторых нефтей.

Кривая течения 2 (см. рис. 3) соответствует жидкостям, у которых отношение напряжения сдвига к скорости сдвига τ постоянно по­нижается с ростом скорости сдвига. Кривая течения становится линейной только при больших скоростях сдвига. Реологическую модель та­кой жидкости впервые предложил Оствальд, и математически ее мож­но записать в виде степенного закона

 

где к и b - постоянные для данной жидкости;

к - мера консистенции жидкости;

b - характеризует степень неньютоновского поведения жидкости

Жидкости, подчиняющиеся этому реологическому закону, назы­ваются псевдопластичными. К ним относятся жидкости, содержащие некрупные мехпримеси, суспензии, растворы высокополимеров.

С целью возможности применения имеющихся формул реологии, выведенных для ньютоновских жидкостей (в основном, для воды), для неньютоновских сред вводится понятие кажущейся вязкости - μ или эффективной – μ _э. Тогда для неныотоновской жидкости можно запи­сать следующее выражение:

Из сравнения (6) и (5) получим

Из рис. 3 видно, что μ _э определяется отношением отрезков ON и

ОМ, следовательно, для каждого значения имеет свое значение.

Эффективная вязкость псевдопластичных жидкостей с увеличением скорости сдвига снижается. Это можно объяснить тем, что при движе­нии перемещение отдельных частиц или молекул становится ориенти­рованным вдоль потока. Эффективная вязкость будет убывать до тех пор, пока сохраняется возможность дальнейшей ориентации частиц вдоль линии тока, а затем кривая становится линейной.

Реологическому закону (5) подчиняется и жидкость, представлен­ная кривой течения 3 на рис. 3, но показатель " Ь" для этих жидкостей превышает

Такой тип течения был впервые обнаружен Рейнольдсом в сус­пензиях с большим содержанием твердой фазы. Для этой жидкости ха­рактерно увеличение эффективной вязкости с увеличением скорости сдвига. Это объясняется тем, что при движении дилатантных жидкостей крупные частицы мехпримесей с увеличением скорости сдвига начинают ударяться друг о друга, а на удар тратится значительная часть энергии.

Для многих жидкостей в широком диапазоне изменения скорости сдвига касательные напряжения хорошо описываются реологической моделью нелинейного вязкопластика

 

 

Данная модель является общим вариантом рассмотренных ранее (см. рис. 3, кривые течения 4, 5). В частном случае, если τ _о=0, то имеем реологическое уравнение (5); если К=μ., b=1, то получим модель Шведова-Бингама. При τ _о=0, К=μ., b=1 получаем закон Ньютона.

Для многих реальных жидкостей кажущаяся вязкость определяется­
не только скоростью сдвига, но и продолжительностью сдвига. Эти
жидкости называются нереостабильными и в зависимости от характера изменения кривой течения во времени подразделяются на тиксотропные и реопектические.

Тиксотропными называются материалы, консистенция которых зависит от продолжительности сдвига и величины скорости сдвига.

Если тиксотропный материал, находящийся в состоянии покоя, деформировать с постоянной скоростью сдвига, то его структура будет постепенно разрушаться, а эффективная вязкость и касательные на­пряжения снижаться со

 

Рис. 4. График зависимости от времени

 

временем. На рис. 4 представлен график зави­симости касательных напряже­ний т при постоянном градиенте скорости сдвига от времени t. Линия 1 принадлежит реостабильным жидкостям. Линия 3 - тиксотропным. Тиксотропию проявляют нефти и нефтепро­дукты с большим содержанием парафина, глинистые растворы. Тиксотропия является об­ратимым процессом, после исчезновения возмущения ее касательных напряжений структура постепенно восстанавливается.

Если снимать кривые течения, повторяя опыты друг за другом, то для тиксотропной жидкости будет наблюдаться изменение кривой течения от опыта к опыту (рис. 5).

Рис. 5. Кривые течения тиксотропных жидкостей

Если снять кривую течения тиксотропной жидкости сначала для равномерного возрастания градиента скорости сдвига, а затем с рав­номерным убыванием, то получим кривую течения, представленную на рис. 6 в виде гистерезисной петли.

Рис. 6. Гистерезисные петли тиксотропной жидкости:

1 - с ненарушенной или частично разрушенной структурой;

2 - с полностью разрушенной структурой

Если с увеличением времени при фиксированной скорости сдвига касательные напряжения увеличиваются, жидкость называется реопектической (см. кривую 2, рис. 4). Реопексию проявляет, например, 40 % -ный раствор гипса. По-видимому, при малых скоростях сдвига более бла­гоприятные условия образования структуры (но и термический эф­фект).