Лекция 7. Матричные преобразования систем координатПреобразования, связанные с системой координат Необходимо научиться управлять изображением на экране, вносить изменения в его положение, форму, ориентацию, размер. Для этих целей существуют специальные геометрические преобразования, которые позволяют изменять эти характеристики объектов в пространстве. Представим задачу создания компьютерного имитатора полетов на военном самолете. Объекты на земле, как и сам самолет, изменяют свое положение: вращается антенна локатора, движется танк. При этом, наблюдатель видит эту картину из определенной точки в пространстве в выбранном направлении. Необходимо описать эти сложные преобразования математически. Введем три вида систем координат. Первая из них – мировая система координат – задается осями 1. Преобразовать координаты объекта, заданные в собственной системе координат, в мировые координаты. 2. Преобразовать координаты объекта, заданные уже в мировой системе координат, в систему координат наблюдателя. 3. Спроецировать полученные координаты на проекционную плоскость в системе координат наблюдателя. Отметим, определенную двойственность впечатлений, возникающих при взаимных перемещениях систем координат друг относительно друга. Представим себе, что мы наблюдаем кубик в пространстве. Пусть теперь этот кубик начнет вращаться вокруг, например, вертикальной оси. Мы увидим, что кубик вращается. Но тот же самый эффект мы получим, если сами начнем облетать вокруг кубика и рассматривать его с разных сторон. Визуальный эффект остается тем же самым, хотя в первом случае наша система координат остается неподвижной, а во втором – вращается по орбите. Этот эффект можно использовать при выводе формул движения в пространстве.
|
. Мы размещаем ее в некоторой точке, и она остается неподвижной всегда. Вторая – система координат наблюдателя. Эту систему назовем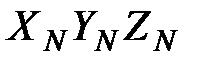 
. Она определяет положение наблюдателя в пространстве и задает направление взгляда. И третья – система координат объекта. В нашем случае их две: система координат локатора и система координат танка. Эти системы также могут перемещаться и изменять свое положение в пространстве относительно мировой системы координат. Координаты точек объектов задаются в системах координат объектов, каждая из которых, в свою очередь, привязана к мировой системе координат. Система координат наблюдателя также перемещается относительно мировой системы координат. Теперь становится понятно, что для того, чтобы увидеть трехмерный объект на экране компьютера надо проделать следующие шаги.
