Однородные координаты и матричное представление двумерных преобразований
В предыдущем параграфе были рассмотрены три вида преобразований точек на плоскости. Два из них – операции вращения и масштабирования - описываются в виде произведения матрицы на вектор, а третья – операция переноса – описывается как сумма двух векторов. В случае последовательного выполнения любой комбинации операций вращения и масштабирования результат легко можно записать в виде произведения матриц соответствующих преобразований. Это будет матрица результирующего поворота и масштабирования. Очевидно, что удобнее применять результирующую матрицу вместо того, чтобы каждый раз заново вычислять произведение матриц. Однако, таким способом нельзя получить результирующую матрицу преобразования, если среди последовательности преобразований присутствует хотя бы один перенос. Матричное произведение в компьютерной графике также называют композицией. Было бы удобнее иметь математический аппарат, позволяющий включать в композиции преобразований все три выше указанные операции. При этом получился бы значительный выигрыш в скорости вычислений. Однородные координаты и есть этот математический аппарат. Двумерный вектор В общем случае осуществляется переход от n -мерного пространства к Рассмотрим некоторые свойства однородных координат. Некоторые точки, неопределенные в n-мерном пространстве, становятся вполне определенными при переходе к однородным координатам. Например, однородный вектор Рассмотрим точку трехмерного пространства
Рис. 4. Проекция точки
Аналогично, рассматривая применение однородных координат для векторов трехмерного пространства, можно представить трехмерное пространство как проекцию четырехмерного пространства на гиперплоскость В однородных координатах преобразование центральной перспективы можно определить матричной операцией. Эта матрица записывается в виде:
Покажем, что эта матрица определяет преобразование точки объекта, заданной в однородных координатах, в точку перспективной проекции (также в однородных координатах). Пусть
Теперь точки двумерного пространства будут описываться трехэлементными вектор-строками, поэтому и матрицы преобразований, на которые будет умножаться вектор точки, будут иметь размеры 3´ 3. Запишем матричное преобразование операции переноса для однородных координат:
или При последовательном переносе точки
Запишем матричный вид операции масштабирования.
Определим матрицу масштабирования Так же, как последовательные переносы являются аддитивными, покажем, что последовательные масштабирования будут мультипликативными.
Для операции поворота матричный вид будет такой:
Определим матрицу поворота Аналогично двум предыдущим случаям, покажем, что матрица поворота остается таковой при последовательных поворотах.
Таким образом, доказано, что два, а значит и любое количество последовательных поворотов можно записать в виде одной матрицы суммарного поворота. Также легко заметить, что любая последовательность операций, включающая в себя перенос, масштабирование и вращение в однородных координатах, может быть представлена одной матрицей, которая является произведением матриц данных операций. Рассмотрим, каким образом с помощью композиции матричных преобразований можно получить одно общее результирующее преобразование. Для этого будем использовать матрицы T, S и R. С вычислительной точки зрения гораздо проще и быстрее применять матрицу уже готового преобразования вместо того, чтобы применять их последовательно одну за другой. К точке более эффективно применять одно результирующее преобразование, чем ряд преобразований друг за другом. Для примера рассмотрим задачу поворота объекта на плоскости относительно некоторой произвольной точки Вот эта последовательность элементарных преобразований (рис. 5): 1. Перенос, при котором точка 2. Поворот на заданный угол. 3. Перенос, при котором точка из начала координат возвращается в первоначальное положение
Рис. 5. Последовательность преобразований при повороте объекта вокруг точки
Точка
|

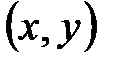 в однородных координатах записывается в виде
в однородных координатах записывается в виде  , где
, где  . Число
. Число  называется масштабным множителем. Для того, чтобы из вектора, записанного в однородных координатах получить вектор в обычных координатах необходимо разделить первые две координаты на третью:
называется масштабным множителем. Для того, чтобы из вектора, записанного в однородных координатах получить вектор в обычных координатах необходимо разделить первые две координаты на третью:  .
.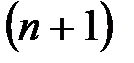 -мерному. Это преобразование не единственное. Обратное преобразование называется проекцией однородных координат*.
-мерному. Это преобразование не единственное. Обратное преобразование называется проекцией однородных координат*. в трехмерном пространстве соответствует бесконечно удаленной точке
в трехмерном пространстве соответствует бесконечно удаленной точке  . Поскольку в однородных координатах эту точку можно представить в виде
. Поскольку в однородных координатах эту точку можно представить в виде  , при
, при  , то в трехмерном пространстве это соответствует точке
, то в трехмерном пространстве это соответствует точке  .
. . Если представить эту точку как однородное представление точки двумерного пространства, то ее координаты будут
. Если представить эту точку как однородное представление точки двумерного пространства, то ее координаты будут  . Сравнивая эти координаты со вторым видом формул, выведенных для центральной перспективной проекции, легко заметить, что двумерное представление точки с координатами
. Сравнивая эти координаты со вторым видом формул, выведенных для центральной перспективной проекции, легко заметить, что двумерное представление точки с координатами  выглядит как ее проекция на плоскость
выглядит как ее проекция на плоскость 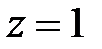 , как показано на рис. 4.
, как показано на рис. 4.
 на плоскость
на плоскость 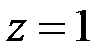 .
. , если
, если  .
.
 – точка в трехмерном пространстве. Ее однородное представление
– точка в трехмерном пространстве. Ее однородное представление 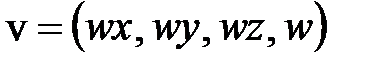 . Умножим v на P:
. Умножим v на P: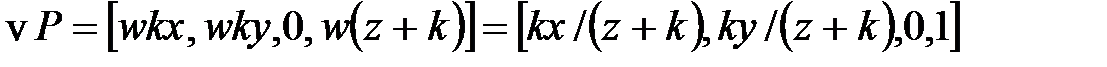

 , где
, где 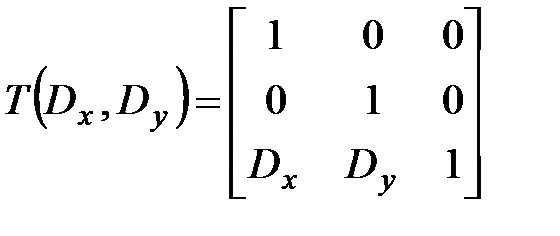 .
.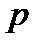 в точку
в точку 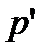 и затем в точку
и затем в точку 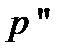 компоненты суммарного вектора переноса являются суммами соответствующих компонент последовательных векторов переноса. Рассмотрим, каковы будут элементы матрицы суммарного переноса. Пусть
компоненты суммарного вектора переноса являются суммами соответствующих компонент последовательных векторов переноса. Рассмотрим, каковы будут элементы матрицы суммарного переноса. Пусть  ,
,  . Подставив первое уравнение во второе получаем
. Подставив первое уравнение во второе получаем  . Матричное произведение т.е. суммарный перенос равен произведению соответствующих матриц переноса.
. Матричное произведение т.е. суммарный перенос равен произведению соответствующих матриц переноса.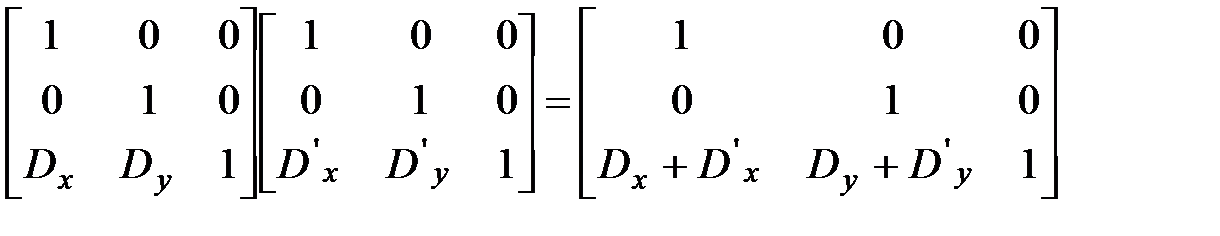
 .
.


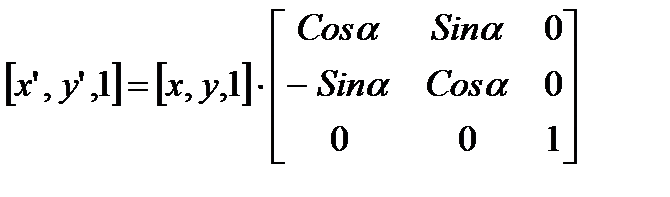
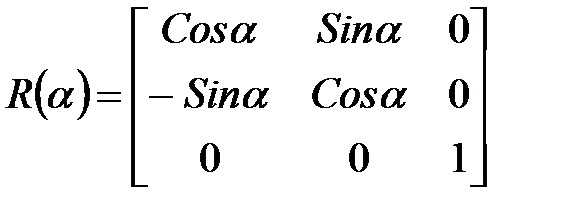
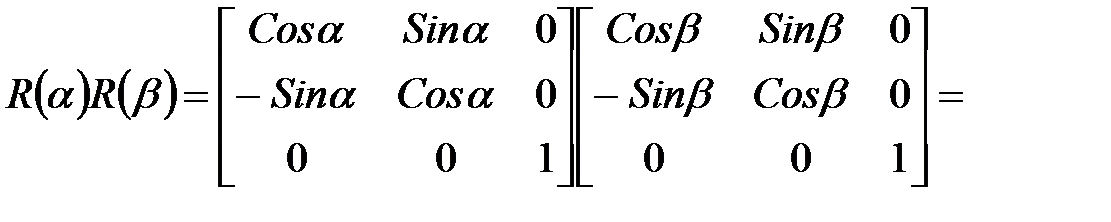

 . Пока мы умеем поворачивать объекты только вокруг начала координат. Но можно представить эту задачу как последовательность шагов, на каждом из которых будет применяться только элементарная операция: перенос, масштабирование или вращение.
. Пока мы умеем поворачивать объекты только вокруг начала координат. Но можно представить эту задачу как последовательность шагов, на каждом из которых будет применяться только элементарная операция: перенос, масштабирование или вращение.
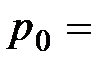
 на угол a.
на угол a. , а обратный перенос ‑ на вектор
, а обратный перенос ‑ на вектор  .
.


