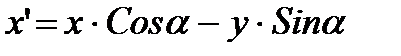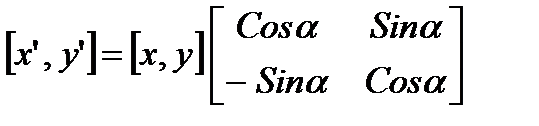Двумерные матричные преобразования
Рассмотрим преобразования координат точек на плоскости. На рис. 1 точка
Рис. 1. Операция переноса или трансляции точки
Математически этот перенос можно описать с помощью вектора переноса
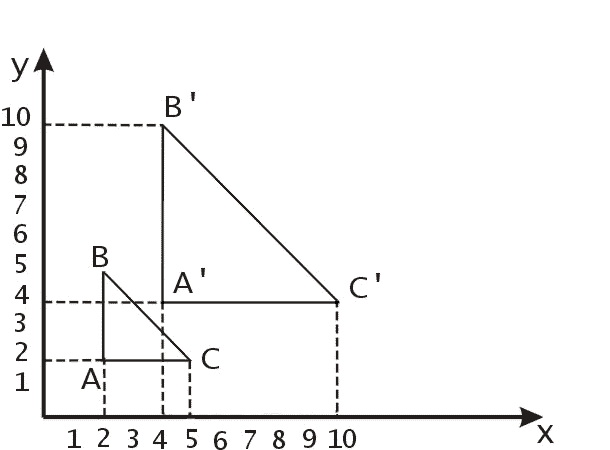
Масштабированием объектов называется растяжение объектов вдоль соответствующих осей координат относительно начала координат. Эта операция применяется к каждой точке объекта, поэтому можно также говорить о масштабировании точки. При этом, конечно, речь не идет об изменении размеров самой точки. Масштабирование достигается умножением координат точек на некоторые константы. В том случае, когда эти константы равны между собой, масштабирование называется однородным. На рис.2 приведен пример однородного масштабирования треугольника
Рис. 2. Операция масштабирования.
После применения операции однородного масштабирования с коэффициентом 2 он переходит в треугольник
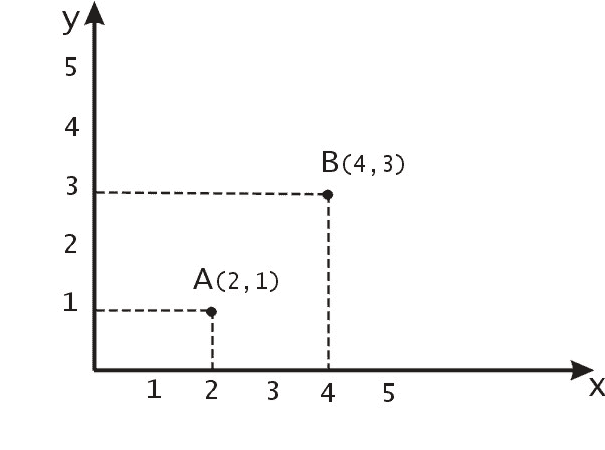
Рассмотрим далее операцию вращения точки на некоторый угол относительно начала координат. На рисунке 3 точка
Рис. 3. Операция поворота точки
Найдем преобразование координат точки А в точку В. Обозначим
Так как
В матричном виде вращение точки А на угол
|

 перенесена в точку
перенесена в точку  .
.
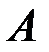 в точку
в точку 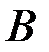 .
. . Пусть
. Пусть 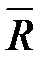 радиус вектор, соответствующий вектору переноса
радиус вектор, соответствующий вектору переноса 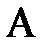 в точку
в точку  будет соответствовать векторной записи
будет соответствовать векторной записи  . Отсюда получаем, что для переноса точки в новое положение необходимо добавить к ее координатам некоторые числа, которые представляют собой координаты вектора переноса:
. Отсюда получаем, что для переноса точки в новое положение необходимо добавить к ее координатам некоторые числа, которые представляют собой координаты вектора переноса:
 .
.
 . Обозначим матрицу масштабирования
. Обозначим матрицу масштабирования 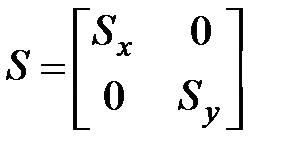 . Для точек
. Для точек 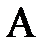 и
и 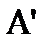 операция масштабирования в матричном виде будет выглядеть следующим образом:
операция масштабирования в матричном виде будет выглядеть следующим образом: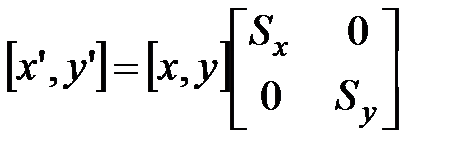 .
. переходит в точку
переходит в точку 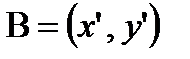 поворотом на угол
поворотом на угол 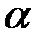 .
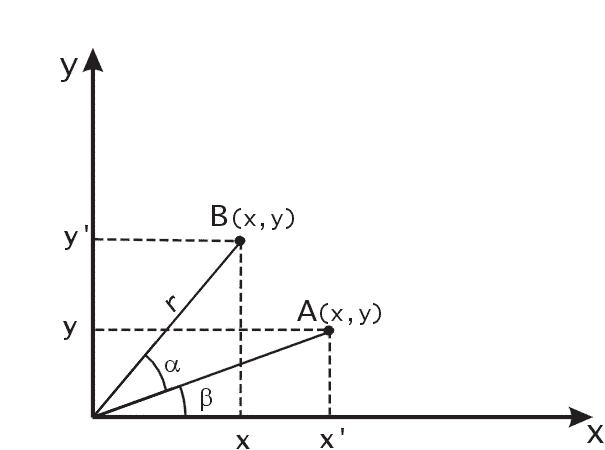
.
 .
.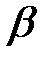 угол, который составляет радиус-вектор
угол, который составляет радиус-вектор 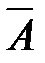 с осью О x. Пусть r – длина радиус-вектора
с осью О x. Пусть r – длина радиус-вектора 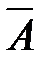 , тогда
, тогда

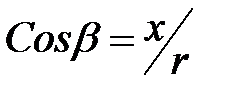 и
и 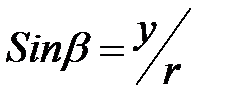 , то подставляя эти выражения в уравнения для
, то подставляя эти выражения в уравнения для 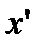 и
и 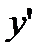 , получаем:
, получаем: