Примеры. Пример 1. Выяснить, сходится или расходится ряд
Пример 1. Выяснить, сходится или расходится ряд Данный ряд знакоположительный. Сравним его с гармоническим рядом
По первому признаку сравнения из расходимости гармонического ряда следует расходимость данного ряда. Замечание. Расходимость данного ряда можно доказать с помощью интегрального признака или просто указать, что ряд Пример 2. Выяснить, сходится или расходится ряд
Данный ряд знакоположительный. Сравним его с рядом
По первому признаку сравнения сравним соответствующие члены двух рядов:
Так как члены данного ряда меньше соответствующих членов сходящегося ряда Пример 3. Выяснить, сходится или расходится ряд
Данный ряд является знакоположительным. Применим второй признак сравнения, для сравнения возьмём гармонический ряд
По второму признаку сравнения данный ряд и гармонический ведут себя одинаково, т. е. из расходимости гармонического следует, что и данный ряд расходится. Пример 4. Исследовать, сходится или расходится ряд
Данный ряд перепишем в виде Пример 5. С помощью интегрального признака доказать сходимость ряда
Общий член ряда
Так как интеграл сходится, то сходится и данный ряд. Замечание. Сходимость данного ряда можно доказать также по второму признаку сравнения, взяв для сравнения ряд Дирихле Пример 6. С помощью признака Даламбера выяснить, сходится или расходится ряд
Общий член ряда
Но e > 2, значит, Пример 7. Применяя признак Коши, исследовать, сходится или расходится ряд
Общий член ряда
Так как предел Замечание. Расходимость этого ряда можно доказать иначе. Ряд расходится, так как не выполнен необходимый признак сходимости:
|

 .
. , который расходится. Члены данного ряда больше соответствующих членов гармонического ряда:
, который расходится. Члены данного ряда больше соответствующих членов гармонического ряда:
 . Так как p < 1, то ряд расходится.
. Так как p < 1, то ряд расходится. .
. , который является сходящейся геометрической прогрессией с
, который является сходящейся геометрической прогрессией с .
. .
. .
. .
.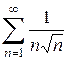 .
. . Это – ряд Дирихле при
. Это – ряд Дирихле при  . Так как p > 1, то данный ряд сходится.
. Так как p > 1, то данный ряд сходится. .
. . Записывая в этой формуле x вместо n, получаем функцию
. Записывая в этой формуле x вместо n, получаем функцию  . Эта функция удовлетворяет условиям интегрального признака: она принимает положительные значения и убывает с возрастанием x. Вычислим
. Эта функция удовлетворяет условиям интегрального признака: она принимает положительные значения и убывает с возрастанием x. Вычислим .
. , сходящийся, так как p = 2 > 1.
, сходящийся, так как p = 2 > 1. .
. . Заменяя всюду n на (n + 1), получим:
. Заменяя всюду n на (n + 1), получим:  . Находим:
. Находим: ;
; .
. > 1, откуда, согласно признаку Даламбера, ряд расходится.
> 1, откуда, согласно признаку Даламбера, ряд расходится. .
. .
. ;
; .
. > 1, то, согласно признаку Коши, ряд расходится.
> 1, то, согласно признаку Коши, ряд расходится. .
.


