Необходимый признак сходимости
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
Пусть задана некоторая бесконечная последовательность чисел
Тогда выражение
называется числовым рядом, а сами числа
Если существует предел S бесконечной последовательности чисел
то этот предел называют суммой ряда (1), а сам ряд (1) в этом случае называется сходящимся. Если же предел Пусть ряд (1) сходится. Тогда его частичная сумма
называется остатком ряда. Этот остаток является суммой ряда:
Если ряд (1) сходится, то
Бесконечная геометрическая прогрессия
есть сходящийся числовой ряд, если
В случае Если ряд (1) имеет сумму S, то ряд
сходится и имеет сумму Сходящиеся ряды можно почленно складывать и вычитать, т. е., если даны сходящиеся ряды
то ряды
тоже сходятся, и суммы их соответственно равны Свойство сходимости или расходимости ряда не нарушается, если отбросить или прибавить к нему любое конечное число членов. Необходимый признак сходимости ряда: Если ряд (1) сходится, то его общий член стремится к нулю при
Обратное утверждение неверно. Из того, что Пример 1. Члены ряда Пример 2. Члены ряда
С помощью необходимого признака сходимости нельзя доказать сходимость ряда, но иногда удаётся доказать расходимость, применяя следствие из необходимого признака, которое легко доказывается от противного. Следствие из необходимого признака сходимости: Если Пример 3. Выяснить, сходится или расходится ряд
Общий член этого ряда Пример 4. Проверить, выполняется ли необходимый признак сходимости для ряда
Исследование сходимости рядов, как правило, сводится к вычислению некоторых пределов, при этом часто используются известные условия эквивалентности бесконечно малых, которые применительно к рядам принимают вид при
Часто также приходится иметь дело с пределами:
|


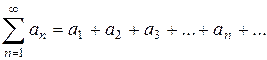 (1)
(1)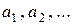 – членами ряда. Сумма n первых членов ряда называется n -й частичной суммой ряда и обозначается
– членами ряда. Сумма n первых членов ряда называется n -й частичной суммой ряда и обозначается 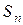 :
: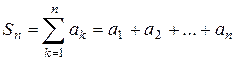 . (2)
. (2)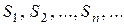 , т. е.
, т. е.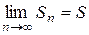 , (3)
, (3) не существует, то ряд (1) называют расходящимся. Расходящийся ряд суммы не имеет. Однако, если
не существует, то ряд (1) называют расходящимся. Расходящийся ряд суммы не имеет. Однако, если 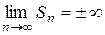 , то иногда говорят, что ряд (1) имеет бесконечную сумму.
, то иногда говорят, что ряд (1) имеет бесконечную сумму.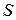 . Погрешность этого приближения
. Погрешность этого приближения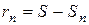 (4)
(4) (5)
(5) .
. (6)
(6) . Сумма ряда (6) равна в этом случае
. Сумма ряда (6) равна в этом случае .
. ряд (6) расходится.
ряд (6) расходится.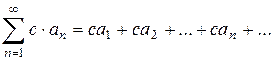 (7)
(7)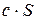 . Если же ряд (1) расходится, то (при
. Если же ряд (1) расходится, то (при  ) расходится и ряд (7).
) расходится и ряд (7). (8)
(8)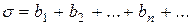 , (9)
, (9)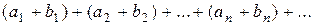 (10)
(10)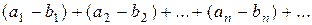 (11)
(11) и
и 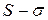 .
.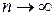 , т. е.
, т. е. .
. , сходимость ряда
, сходимость ряда 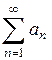 не следует. Для сходимости ряда общий член ряда должен не просто стремиться к нулю, но делать это достаточно быстро.
не следует. Для сходимости ряда общий член ряда должен не просто стремиться к нулю, но делать это достаточно быстро. , называемого гармоническим, стремятся к нулю с ростом их номеров (
, называемого гармоническим, стремятся к нулю с ростом их номеров ( ), однако этот ряд расходится, его
), однако этот ряд расходится, его 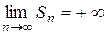 . (Расходимость может быть доказана интегральным признаком).
. (Расходимость может быть доказана интегральным признаком).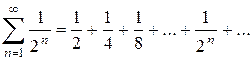 тоже стремятся к нулю с ростом их номеров (
тоже стремятся к нулю с ростом их номеров ( ), но убывают быстрее, чем члены гармонического ряда. Этот ряд уже является сходящимся, его сумма может быть найдена по формуле суммы бесконечно убывающей геометрической прогрессии:
), но убывают быстрее, чем члены гармонического ряда. Этот ряд уже является сходящимся, его сумма может быть найдена по формуле суммы бесконечно убывающей геометрической прогрессии: .
.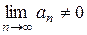 , то ряд расходится.
, то ряд расходится.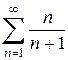 .
.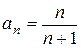 .
. 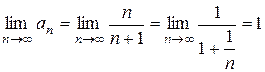 , т. е.
, т. е. 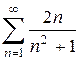 .
. . Необходимый признак выполняется, поэтому ряд может быть как сходящимся, так и расходящимся, что можно установить лишь после дополнительного исследования.
. Необходимый признак выполняется, поэтому ряд может быть как сходящимся, так и расходящимся, что можно установить лишь после дополнительного исследования. ,
, ,
,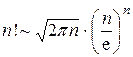 (формула Стирлинга).
(формула Стирлинга).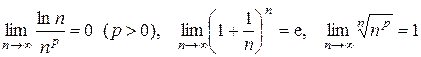 .
.


