Степенные ряды
Степенным рядом называется функциональный ряд вида
где
Теорема Абеля. 1) Если ряд (2) сходится при 2) Если ряд (2) расходится при Область сходимости степенного ряда (2) есть симметричный относительно начала координат O интервал (– R, R), называемый интервалом сходимости ряда (2). Число Радиус сходимости может быть вычислен по формулам
или
Степенной ряд (2) внутри интервала сходимости сходится абсолютно. Вне интервала сходимости ряд (2) расходится. При x = – R или x = R ряд (2) может оказаться расходящимся, сходящимся условно или сходящимся абсолютно. Степенной ряд (1) сходится абсолютно на интервале (a – R, a + R). На всяком отрезке, целиком лежащем внутри интервала сходимости, сумма степенного ряда есть непрерывная функция. Если пределы интегрирования α, β лежат внутри интервала сходимости степенного ряда, то определённый интеграл от суммы ряда в этих пределах равен сумме таких же интегралов от членов ряда. Интервал сходимости нового ряда остаётся прежним. Пусть
– степенной ряд, имеющий интервал сходимости (– R, R). Тогда ряд
сходится на том же интервале, и его сумма Простейшим примером степенного ряда является геометрическая прогрессия
(в соответствии с формулой
Пример 1. Найти радиус и интервал сходимости степенного ряда
Применим формулу (4):
R = ∞, значит, ряд сходится при всех x, т. е. в интервале (– ∞, + ∞). Заметим для дальнейшего, что из сходимости ряда вытекает: Пример 2. Найти область сходимости степенного ряда
Радиус сходимости найдём по признаку Даламбера:
Таким образом, ряд сходится на интервале 1) На левом конце ряд принимает вид
По теореме Лейбница, ряд на левом конце интервала сходится. 2) На правом конце интервала ряд принимает вид
Это – ряд Дирихле при Таким образом, область сходимости ряда есть промежуток
|

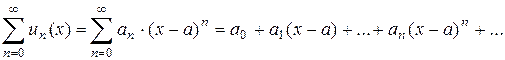 , (1)
, (1)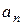 (n = 0, 1, 2, …) – числа, называемые коэффициентами ряда. При a = 0 ряд принимает вид
(n = 0, 1, 2, …) – числа, называемые коэффициентами ряда. При a = 0 ряд принимает вид (2)
(2) , то он абсолютно сходится при любом значении x, удовлетворяющем неравенству
, то он абсолютно сходится при любом значении x, удовлетворяющем неравенству  .
. , то он расходится и при любом значении x, для которого
, то он расходится и при любом значении x, для которого  .
. называется радиусом сходимости ряда (2).
называется радиусом сходимости ряда (2). (3)
(3) . (4)
. (4)
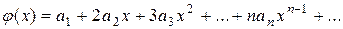
 при
при  .
. . Этот ряд сходится при
. Этот ряд сходится при  . Следовательно, для данного ряда радиус сходимости R = 1, а интервалом сходимости является интервал (–1, 1). Сумма этого ряда равна
. Следовательно, для данного ряда радиус сходимости R = 1, а интервалом сходимости является интервал (–1, 1). Сумма этого ряда равна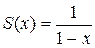
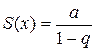 , a = 1, q = x). Поэтому для функции
, a = 1, q = x). Поэтому для функции  (5)
(5) .
. .
. при всех x.
при всех x. .
. .
.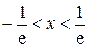 . Исследуем сходимость ряда на концах интервала:
. Исследуем сходимость ряда на концах интервала: , т. е. является знакочередующимся. Абсолютная величина его общего члена
, т. е. является знакочередующимся. Абсолютная величина его общего члена 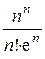 с учётом формулы Стирлинга (стр. 4) эквивалентна при n → ∞
с учётом формулы Стирлинга (стр. 4) эквивалентна при n → ∞ .
. ;
; .
. , поэтому данный ряд на правом конце своего интервала сходимости расходится.
, поэтому данный ряд на правом конце своего интервала сходимости расходится. .
.


