III. РЯДЫ ФУРЬЕ
1. Рядом Фурье функции f (x), определённой на отрезке [–π, π ], называется ряд
коэффициенты которого определяются по формулам
При этом пишут
Поскольку построение ряда (1.2) выполнено формально, то этот ряд может расходиться или сходиться, но сумма его, вообще говоря, может не совпадать с разложенной в него функцией. 2.Сформулируем достаточные условия, при выполнении которых ряд (1.2) имеет сумму, равную заданной функции f (x): Функция f (x) может иметь на отрезке [–π, π ] лишь конечное число максимумов и минимумов и должна быть непрерывной, за исключением, быть может, конечного числа точек разрыва первого рода. Эти условия называются условиями Дирихле. Теорема Дирихле. Если функция f (x) удовлетворяет условиям Дирихле на отрезке [–π, π ], то её ряд Фурье сходится к функции f (x) во всех точках, в которых она непрерывна. В точках разрыва функции ряд сходится к полусумме 3. Пусть теперь функция f (x) задана на отрезке [– l, l ]. Ряд Фурье в этом случае имеет вид
где
Вопрос о сходимости ряда (3.1), в свою очередь, определяется теоремой Дирихле, но на отрезке [– l, l ], соответственно. Суммой ряда будет периодическая на всей числовой оси функция с периодом 2 l. Замечание: Значок ~ в (1.2) и (3.1) нужно понимать следующим образом: если f (x) удовлетворяет условиям Дирихле на [–π, π ] и [– l, l ] соответственно, то во всех точках её непрерывности значок ~ надо заменить знаком = и помнить, что в точках разрыва сумма ряда равна полусумме левого и правого пределов f (x) в этих точках, а на концах отрезка – Пример 1. Разложить функцию
в ряд Фурье на интервале (–2, 2). Рис. 1
= =
= Таким образом, разложение функции f (x) в ряд Фурье имеет вид
В соответствии с теоремой Дирихле, график суммы ряда Фурье для функции f (x) имеет вид Рис. 2 4. Разложение в ряд Фурье чётных и нечётных функций. а) Пусть функция f (x), заданная на отрезке [– l, l ] – чётная и удовлетворяет условиям Дирихле. Тогда ряд Фурье для этой функции будет содержать только
Пример 2. Разложить в ряд Фурье на отрезке [–π, π ] чётную функцию f (x) = | x |. Рис. 3 Данная функция непрерывна на заданном отрезке (l = π) и имеет на нём один экстремум, поэтому удовлетворяет условиям Дирихле. Ряд (4.1) в данном случае принимает вид
Так как f (x) = | x | = x при 0 ≤ x ≤ π, то
= =
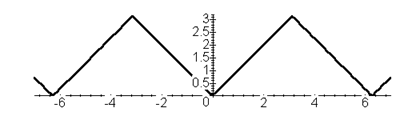
В соответствии с теоремой Дирихле, график суммы ряда Фурье – периодическая функция с периодом 2π, которая совпадает с f (x) на отрезке
[–π, π ] (рис. 4). Рис. 4 На рис. 5 изображены графики частичных сумм ряда Фурье = –
Рис. 5 б) Пусть функция f (x), заданная на отрезке [– l, l ] – нечётная и удовлетворяет условиям Дирихле. Тогда ряд Фурье для этой функции будет содержать только члены с синусами:
где
Пример 3. Разложить в ряд Фурье на отрезке [–2, 2] нечётную функцию f (x) = x. Рис. 6 Эта функция на заданном отрезке удовлетворяет условиям Дирихле, так как непрерывна и не имеет там экстремумов. Ряд Фурье для данной функции имеет вид
где = =
На рис. 7 изображены графики частичных сумм ряда Фурье
=  , ,  = =  , ,  = =  + +
+ Рис. 7 5. Разложение в ряд Фурье функций, заданных на отрезке [0, l ]. В этом случае можно доопределить функцию на полуинтервал [– l, 0) либо чётным, либо нечётным образом. В первом случае получится чётная на [– l, l ] функция, которая будет раскладываться в ряд Фурье по косинусам, а во втором – нечётная на [– l, l ] функция, и её ряд Фурье будет содержать только синусы. В обоих случаях на отрезке [0, l ] эти ряды дадут разложение исходной функции в ряд Фурье. Пример 4. Разложить функцию f (x) = x, заданную на отрезке [0, π ], доопределив её чётным образом на полуинтервал [–π, 0). В результате получим чётную функцию φ (x); для x < 0 будет φ (x) = = φ (– x) = f (– x) = – x, следовательно, φ (x) = | x | на [–π, π ]. Разложение этой функции было сделано в примере 2, и оно одновременно является разложением f (x) = x на отрезке [0, π ]. Пример 5. Разложить функцию f (x) = x + 1, заданную на отрезке [0, 2], в ряд Фурье, продолжив её нечётным образом на полуинтервал [-2, 0)
Рис. 8 В результате получим нечётную функцию φ (x); для x < 0 будет φ (x) = – φ (– x) = – f (– x) = x – 1, следовательно, φ (x) = φ (x) = где
φ (x) = В этот ряд одновременно разложена заданная на [0, 2] функция f (x) = x + 1. Замечание: Можно также разложить f (x) и на отрезке [0, l ], но тогда в разложение войдут члены ряда и с синусами, и с косинусами, а сумма ряда будет периодической функцией с периодом T = l.
|

 ,
, ,
, ,
, (1.1)
(1.1) (1.2)
(1.2) её предельных значений слева и справа ( c – точка разрыва первого рода). Если
её предельных значений слева и справа ( c – точка разрыва первого рода). Если  , то в точках
, то в точках  ряд сходится к значению
ряд сходится к значению  . При этом сумма ряда (1.2) является периодической с периодом 2π функцией на всей оси Ox.
. При этом сумма ряда (1.2) является периодической с периодом 2π функцией на всей оси Ox. , (3.1)
, (3.1) ,
, ,
, (3.2)
(3.2)
 , если
, если 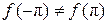 (
( соответственно).
соответственно).

 . Данная функция непрерывна на отрезке [–2, 2] и не имеет там экстремумов, следовательно, удовлетворяет условиям Дирихле. Вычислим коэффициенты ряда:
. Данная функция непрерывна на отрезке [–2, 2] и не имеет там экстремумов, следовательно, удовлетворяет условиям Дирихле. Вычислим коэффициенты ряда: ;
; =
= =
=

 =
=  =
= .
. .
.
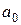 и члены с косинусами, т. е.
и члены с косинусами, т. е. , (4.1)
, (4.1) .
.
 .
. ,
, =
= =
=
 .
.
 =
= ,
,  ,
,  –
–  :
:
 ,
, .
.
 ,
, =
= =
= . Таким образом,
. Таким образом, .
.
 :
:
 Эта функция непрерывна на [–2, 2] за исключением точки x = 0, в которой она имеет разрыв первого рода, т. е. удовлетворяет условиям Дирихле:
Эта функция непрерывна на [–2, 2] за исключением точки x = 0, в которой она имеет разрыв первого рода, т. е. удовлетворяет условиям Дирихле: ,
, =
= =
=  . Таким образом,
. Таким образом, .
.


