Глава 1. Теория функций комплексного переменного (продолжение)
Пусть в ортонормированном репере
Вывод этой формулы предлагается читателю в качестве упражнения, он совершенно аналогичен выводу формулы расстояния от точки до прямой на плоскости, проведенному в пункте в § 2.3, пункт 5.
Глава 1. Теория функций комплексного переменного (продолжение). Степень и формула Муавра, корни порядка n.
Доказательство формулы Эйлера Доказательство или вывод формул Неограниченность в С, пример Логарифм. Доказательство формулы Докажем эту формулу:
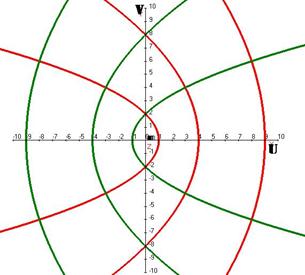
Параграф 2. ФУНКЦИИ Разложение функции f(z) в виде u+iv Чертёж искажений плоскости для
Доказательство, что линейное отображение есть композиция растяжения, поворота и сдвига плоскости Дифференцируемость, условия Коши-Римана.
Аналитичность. Дифференцируемость в точке и её окрестности.
Лекция 2. 9-09-2014
Доказательство потенциальности полей (u, -v), (v, u) для аналитической функции
Метод восстановления одной части аналитической функции по второй её части.
Уравнение Лапласа и его доказательство из условий Коши-Римана. Пример восстановления v(x, y) для u(x, y) =x2-y2. Восстановление f(z)=z2. Интегрирование по кривой. Определение интеграла и метод его вычисления.
Пример вычисления интеграла Первообразная. Формула Ньютона-Лейбница. Пример вычисления интеграла
Лекция 3. 16-09-2014 Интегральная теорема Коши и её доказательство. Интегральная формула Коши + обобщения для степени.
Пример. Нули и особые точки. m- кратный нуль. Полюс порядка m. Классификация: устранимая особая точка, полюс, существенно-особая точка. Вычет функции в точке. Примеры.
ВЫЧЕТЫ для полюса. Вывод формул вычисления вычета для полюса порядка 1 и порядка m: Теорема: Лекция 4. 23-09-2014
|

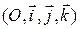 в пространстве
в пространстве  заданы точка
заданы точка 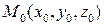 иплоскость
иплоскость 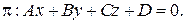 Расстояние
Расстояние 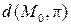 от точки
от точки  до плоскости
до плоскости  выражается формулой:
выражается формулой:
 .
. ,
, 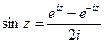 .
.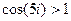
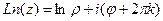 .
.


 , что означает
, что означает 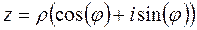 так как синус и косинус не зависят от прибавления угла, кратного
так как синус и косинус не зависят от прибавления угла, кратного 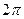 . А это равенство уже очевидно, так как это и есть тригонометрическая форма комплексного числа. Пример
. А это равенство уже очевидно, так как это и есть тригонометрическая форма комплексного числа. Пример 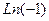 .
.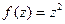 .
.
 ,
, 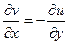 , их доказательство.
, их доказательство.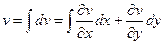 =
=  замены по условиям Коши-Римана.
замены по условиям Коши-Римана. =
=  .
.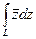 по параболе от 0 до 1+i. Отв.
по параболе от 0 до 1+i. Отв.  .
.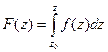 .
. .
.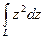 по отрезку от 0 до 1+2i. Отв.
по отрезку от 0 до 1+2i. Отв. 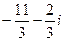 - по формуле Ньютона-Лейбница и без неё.
- по формуле Ньютона-Лейбница и без неё. .
. ,
,  .
.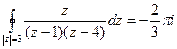 .
.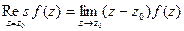 ,
, 
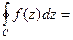
 .
.


