Позиционные системы с произвольным основанием
Метод конечных элементов (МКЭ) – численный метод решения задач прикладной механики деформируемого твёрдого тела, теплообмена, гидродинамики и электромагнитных полей. МКЭ основывается на том, что любое непрерывное распределение физической переменной в расчетной области, например деформацию, можно аппроксимировать набором кусочно-непрерывных функций, определенных на конечном числе подобластей (конечных элементов). Применительно к обработке металлов давлением наиболее широкое распространение получили следующие системы конечно-элементного анализа: холодная листовая штамповка (AutoForm, ANSYS/LS-DYNA), горячая объемная штамповка (DEFORM, qForm, SuperForge). Практически все САПР-программы состоят из отдельных модулей, как правило, специализирующихся на выполнении работы на разных этапах производственного цикла. В модульной структуре систем конечно-элементного анализа выделяют препроцессор, процессор и постпроцессор. В препроцессоре происходит подготовка к процессу вычисления заданных параметров (напряжений, деформаций и т.д.) которая включает в себя: - построение геометрической модели; - указание граничных условий (плоскостей симметрии, контактных поверхностей и т.д.); - представление данных к расчету. В процессоре осуществляется расчет полученных из препроцессора данных, а в постпроцессоре визуализация полученного из процессора результата. Сложность основных алгоритмов. Оценка сложности арифметических операций. Оглавление Позиционные системы с произвольным основанием. 1 Сложность алгоритма(пример Сложность арифметических операций. 4 Оценки функции сложности. 6 Арифметические операции с целыми числами и их сложность. 8 Двоичные операции. 8 Сложение и умножение. 8 Вычитание и деление. 11 О-большое. 12 Теорема (О сравнении операций). 14 Метод Карацубы для оценки сложности операции умножения. 15 Список литературы.. 16
Позиционные системы с произвольным основанием. Опр. Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления. Опр. Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Опр. Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления. Если количество таких цифр равно P, то система счисления называется P -ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления. Теорема. Пусть p > 1 - натуральное число. Тогда для любого n𝜖 N существует n0, n1, …, nS такие что имеет место равенство Доказательство. Пусть n=1, для него есть привычная запись: n0=1, ni=0. Предположим что, существуют числа не имеющие вида (1). Тогда среди таких чисел существует наименьшее число k, причем k¹ 1, а значит Так как Единственность. Из записи вида (1) следует что остаток от деления n на p есть n0, где n0 определенно однозначно. Из выражения Обозначение записи числа в позиционной системе счисления с основанием p. Замечание. Из Теоремы следует способ нахождения вида (3) любого числа. Алгоритм получается следующий: - делим - делим неполное частное снова на
|

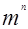 -подсчета достаточного количества операций). 2
-подсчета достаточного количества операций). 2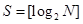
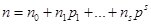 (1), где n0, n1, …, nS принимают значения 0, 1, …, p-1.
(1), где n0, n1, …, nS принимают значения 0, 1, …, p-1.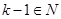 .
.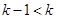 , то для k-1
, то для k-1 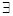 запись вида (1):
запись вида (1):  . Получаем, что
. Получаем, что  , вид типа (1) для k. Наше предположение не верно, теорема доказана.
, вид типа (1) для k. Наше предположение не верно, теорема доказана.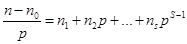 1, получаем, что n1 однозначно определенно как остаток от деления
1, получаем, что n1 однозначно определенно как остаток от деления 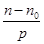 на p. И так далее.
на p. И так далее.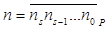 (3), где p основание данной системы счисления., а сама система счисления называется p -ичной.
(3), где p основание данной системы счисления., а сама система счисления называется p -ичной.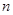 на p получаем остаток
на p получаем остаток 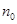 и неполное частное
и неполное частное 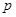 , получаем следующий остаток, и т.д.
, получаем следующий остаток, и т.д.


