О-большое
Определение. Пусть Заметим, что равенство в обозначении f = 0(g) следует, скорее, понимать как неравенство <, а О-большое — как некоторую мультипликативную константу. Пример 3. а) Пусть f(n) - произвольный многочлен степени d с положительным старшим коэффициентом. Тогда, как легко показать, f(n)= O(nd). В более общем случае можно показать, что f = O(g), если f (n)/g(n) имеет конечный предел при n→ ∞. В примере 1 можно записать Time(n!) = O((n logn)2). Функции f (n) и Образно говоря, соотношение f (n)=O(nd) показывает, что функция f растет приблизительно как d-я степень аргумента. Например, если d=3, то оно говорит нам, что удвоение аргумента приведет к увеличению функции приблизительно в 8 раз. Соотношение Заметим, что запись В общем случае, когда оценивается число двоичных операций, требующихся для решения какой-либо задачи, сначала надо определить и выписать подробную процедуру решения задачи. Конкретная пошаговая процедура выполнения вычислений называется алгоритмом. Конечно, может существовать много разных алгоритмов, выполняющих одну и ту же работу. Можно воспользоваться тем из них, который попроще в записи, или тем, который быстрее работает, или выбрать какой-то компромисс между простотой и быстродействием. Использованный выше алгоритм умножения n на m далек от самого быстрого из известных. Но вместе с этим он много быстрее метода повторного сложения (m-кратного сложения числа n с собой). Пример 4. Оценить время, требующееся для перевода числа из k бит в десятичную систему счисления. Решение. Пусть п - целое из к бит, записанное в двоичной системе счисления. Алгоритм перевода следующий. Разделим n на 10 = (1010)2. Остаток от деления — который является одним из чисел 0, 1, 10, 11, 100, 101, 110, 111, 1000 или 1001 — даст содержимое d0 разряда единиц. Частное от деления возьмем вместо n, поделим на (1010)2и возьмем остаток от этого деления в качестве dl а частное — в качестве делимого при следующем делении на (1010)2. Этот процесс должен повторяться столько раз, сколько десятичных разрядов содержится в числе n, т.е. Time (перевод n в десятичную систему счисления) = О (log2 n). Теорема (О сравнении операций) Введем понятия: M(n)– сложность операции умножения 2-х n разрядных чисел. D(n)– сложность операции деления с остатком 2n разрядное на n разрядное. S(n)– сложность операции возведения в квадрат n разрядного числа. R(n)– сложность операции обращение n разрядного числа(под обратным к n разрядному числу N понимается дробь, полученная из Теорема. Пусть функции сложности удовлетворяют следующим условиям: a) f (n)≥ n; и b) kf (n)≤ f (kn) Тогда, если M(n), D(n), S(n), R(n)удовлетворяют а) и б), то M(n)≈ D(n)≈ S(n)≈ R(n). Доказательство: 1)M(n) где 3S(n) - 3 возведения в квадрат, а 4(n)-четыре сложения. 2)S(n) Замечание. Это верно только для точных значений 3) Для доказательства воспользуемся итерационным методом Ньютона для нахождения обратного. Он заключается в вычислении последовательности итераций x(0), x(1), …, x(i), … по формуле: x(i+1)=2x(i)-Nx(i)2. Данная последовательность действительно сходиться к Поэтому при выборе начального значения x(0) так, что 4) 5)
Метод Карацубы для оценки сложности операции умножения. Суть метода заключается в рекурсивном повторении шага: Пусть А и В – два n-разрядных числа. Разобьем их на два слагаемых (для простоты считаем, что Тогда
Таким образом, для вычисления произведения двух n-разрядных чисел нужно выполнить три умножения n/2-разрядных чисел и некоторое количество сложений, вычитаний и переносов. Поэтому для сложности данного алгоритма умножения справедлива оценка
Откуда по Лемме 2
Пример: умножим два числа 1101 и 1011 с помощью метода Карацубы.
Воспользовавшись тождеством представим четырехзначные числа A и B в виде и
Видно, что достаточно произвести всего три умножения двузначных чисел 1101 × 1011=(102 × 11+1) × (102× 10+11)=(104+102)× 11× 10+102× 10× 1+(102+1)× 1× 11=1113111 (Н.Коблиц., 2001)
Список литературы А.В.Черемушкин Лекции по арифметическим алгоритмам в криптографии. [Книга]. - Москва: МЦНМО, 2002. - стр. 104. Н.Коблиц. КУРС ТЕОРИИ ЧИСЕЛ И КРИПТОГРАФИИ. [Книга]. - Москва: Научное изд-во ТВП, 2001. - стр. 254.
|

 и
и  -две функции, определенные на наборах из r положительных целых чисел. Предположим, что существуют такие константы В и С, что, когда все nj больше B, обе функции положительны и
-две функции, определенные на наборах из r положительных целых чисел. Предположим, что существуют такие константы В и С, что, когда все nj больше B, обе функции положительны и  В этом случае говорим, что функция f ограничена функцией g, и пишем f = 0(g).
В этом случае говорим, что функция f ограничена функцией g, и пишем f = 0(g). в качестве исходных данных. Мы хотим получить наши оценки в виде достаточно простых функций g(п). При этом желательно, чтобы функции g (n) не давали чрезмерно завышенное представление о времени решения задач (хотя с чисто математической точки зрения замена функции g(п) в соотношении f =O(g) любой большей функцией корректна).
в качестве исходных данных. Мы хотим получить наши оценки в виде достаточно простых функций g(п). При этом желательно, чтобы функции g (n) не давали чрезмерно завышенное представление о времени решения задач (хотя с чисто математической точки зрения замена функции g(п) в соотношении f =O(g) любой большей функцией корректна). (где
(где  означает
означает  ) показывает, что функция возрастает приблизительно как d-я степень числа двоичных разрядов в п. Это так, потому что с точностью до мультипликативной константы число бит равно приблизительно logn (а именно,
) показывает, что функция возрастает приблизительно как d-я степень числа двоичных разрядов в п. Это так, потому что с точностью до мультипликативной константы число бит равно приблизительно logn (а именно,  ). Так, например, если
). Так, например, если  , то удвоение числа бит в n (что гораздо сильнее увеличивает аргумент, нежели его удвоение) приводит к увеличению f(n) приблизительно в 8 раз.
, то удвоение числа бит в n (что гораздо сильнее увеличивает аргумент, нежели его удвоение) приводит к увеличению f(n) приблизительно в 8 раз. означает, что функция f ограничена некоторой константой.
означает, что функция f ограничена некоторой константой. раз. Тогда процесс будет завершен. Как много двоичных операций будет сделано? Мы сделали О (к) делений, каждое из них требовало O(4к) операций (делимое содержит не более к бит, а делитель (1010)2 - 4 бита). Но О(4к)эквивалентно О(к) (постоянный множитель несуществен в обозначении О-большое). Поэтому общее число двоичных операций равно О(к)× О(к)=O(
раз. Тогда процесс будет завершен. Как много двоичных операций будет сделано? Мы сделали О (к) делений, каждое из них требовало O(4к) операций (делимое содержит не более к бит, а делитель (1010)2 - 4 бита). Но О(4к)эквивалентно О(к) (постоянный множитель несуществен в обозначении О-большое). Поэтому общее число двоичных операций равно О(к)× О(к)=O( ). Если желательно выразить оценку в терминах n, а не k, то, используя равенство
). Если желательно выразить оценку в терминах n, а не k, то, используя равенство  , можно записать
, можно записать отбрасыванием лишних знаков так, чтобы получилось n разрядное число).
отбрасыванием лишних знаков так, чтобы получилось n разрядное число). S(n), так как в силу тождества
S(n), так как в силу тождества  справедлива оценка M(n)≤ 3S(n)+4(n),
справедлива оценка M(n)≤ 3S(n)+4(n), M(n) =O (S(n))Делению на два соответствует операция сдвига.
M(n) =O (S(n))Делению на два соответствует операция сдвига. получаем оценку: S(n)≤ 3R(n)+2n, где 3R(n) - 3 обращения в квадрат, а 2n - два сложения.
получаем оценку: S(n)≤ 3R(n)+2n, где 3R(n) - 3 обращения в квадрат, а 2n - два сложения. :
:
 <
<  (а это легко сделать по двум значащим разрядам N), мы получаем последовательность, в которой каждый раз число правильно вычисленных знаков после запятой удваивается. Благодаря этому мы можем теперь просто заменить нулями те знаки, которым нельзя доверять при данной итерации, и, постоянно удваивая число правильных знаков, через log n шагов получим нужное количество знаков. Отсюда вытекает оценка:
(а это легко сделать по двум значащим разрядам N), мы получаем последовательность, в которой каждый раз число правильно вычисленных знаков после запятой удваивается. Благодаря этому мы можем теперь просто заменить нулями те знаки, которым нельзя доверять при данной итерации, и, постоянно удваивая число правильных знаков, через log n шагов получим нужное количество знаков. Отсюда вытекает оценка: 
 (по лемме1)
(по лемме1)  : из равенства
: из равенства 

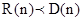 – очевидно
– очевидно По свойству транзитивности, получаем, что включение является замкнутым.
По свойству транзитивности, получаем, что включение является замкнутым.  .
. )
)




 где
где 

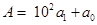
 , где
, где 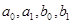 – двузначные числа. Тогда
– двузначные числа. Тогда .
. ,
,  ,
,  , на каждое из которых затратили не больше четырех элементарных умножений, т.е. всего затратим 12 умножений вместо 16 (и некоторое количество сложений). В данном случае: a1=11, a0=1, b1=10, b0=11, откуда
, на каждое из которых затратили не больше четырех элементарных умножений, т.е. всего затратим 12 умножений вместо 16 (и некоторое количество сложений). В данном случае: a1=11, a0=1, b1=10, b0=11, откуда 


