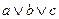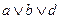Нахождение всех возможных тупиковых форм
Не находя существенных импликант, обозначим все простые импликанты латинскими буквами. Исходная функция может быть записана в виде дизъюнкции простых импликант, что соответствует сокращенной форме (которая является единственной). Эта форма является также тупиковой. Для отыскания всего множества тупиковых форм запишем тождественную логическую формулу:
где Если в формуле Выражение
Тупиковые формы с наименьшим числом букв и есть минимальные формы, тупиковые формы с наименьшим числом членов есть кратчайшие формы. Чаще всего минимальная форма не совпадает с кратчайшей. Рассмотрим на примере 5 этот метод (см. таблицу этапа 2 в методе Квайна). Начертим ее здесь. Обозначив первичные импликанты латинскими буквами a, b, c, d, e, f, а столбцы цифрами (1), (2), …, (8).
Составим функцию
Дизъюнкция
Раскроем скобки
Каждый из членов
Из таблицы следует, что 1-е решение есть минимальная форма (сравните результат), оно же дает кратчайшую форму. Отметим еще раз, что кратчайшая и минимальные формы могут не совпадать. Итак, Замечание 3. Таблица покрытий может не содержать существенных импликаций. Поясним, как в этом случае поступить. Пусть таблица меток имеет вид: (см. ниже). Исключим 2 и 7 столбцы, т.к. 3 и 5 являются их частями, а из оставшихся столбцов выбираем столбец с наименьшим числом меток. Здесь во всех столбцах их по 2, поэтому возьмем 1-й столбец. Примем за псевдосущественную импликанту
Рассмотрим 2 частных случая:
Исключим большие столбцы, содержащие в себе выбранные псевдостолбцы. Запишем множество тупиковых форм для каждой таблицы. Это можно сделать по методу Патрика, но здесь можно перебрать все возможные варианты по таблице
Рассмотрим совместно множества решений. Решение (2) входит в (5), (3) совпадает с (4), а (1) нет соответствующего во 2-й таблице, наиболее простая тупиковая форма (5). Таким образом, разбиение на подтаблицы упрощает отыскание тупиковых форм.
|

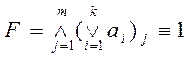
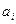 - простые импликанты, соответствующие меткам
- простые импликанты, соответствующие меткам  -го столбца,
-го столбца, 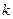 - количество меток в
- количество меток в 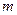 - количество столбцов в таблице меток. Формула
- количество столбцов в таблице меток. Формула 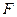 дает полную совершенную нормальную дизъюнктивную форму функции, т.е.
дает полную совершенную нормальную дизъюнктивную форму функции, т.е.  .
.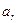 и
и 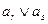 , то член
, то член 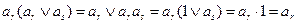 (вот почему на 3 этапе метода Квайна выброшены большие столбцы).
(вот почему на 3 этапе метода Квайна выброшены большие столбцы).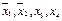
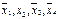
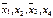
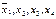

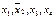
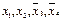
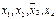
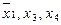
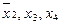
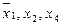

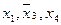
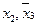

 включается для реализации меток 1-го столбца и т.д. По закону поглощения
включается для реализации меток 1-го столбца и т.д. По закону поглощения  , поэтому члены 3 и 8 можно не записывать. Упростим
, поэтому члены 3 и 8 можно не записывать. Упростим 



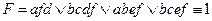
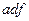

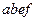
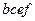
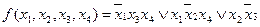 есть минимальная форма данной функции.
есть минимальная форма данной функции. , а затем
, а затем 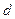 .
.
 2
2

 7
7

 1
1
 c
c
 v
v