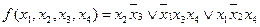Метод. Метод Мак-Класки

 

Этот метод является модернизацией метода Квайна (его 1-го этапа). Мак-Класки предложил записывать исходные импликанты данной функции, заданной в СДНФ, в виде их двоичных кодов (каждому члену ставится в соответствие по известному правилу его собственная вершина). Все множество так записанных импликант разбивается по числу единиц в их кодах на группы. При этом в -ю группу войдут коды, имеющие в своей записи единиц. Попарное сравнение импликант достаточно производить только между соседними группами, т.к. только эти группы отличаются одним знаком в кодах входящих в них членов. Сравнивая коды членов соседних групп, образуют члены низшего ранга. На месте исключенного знака пишут в них “тире”. Затем всю совокупность членов низшего ранга снова разбивают на группы по местоположению знака “тире”.Снова сравнивают члены соседних групп, но уже внутри групп, образуя члены низшего ранга по тому же правилу и т.д.

Далее все производится по методу Квайна, но в кодовых значениях импликант. Рассмотрим это на примере 6.

 

Заменим исходные импликанты их кодами в двоичных переменных: 0011, 0100, 0101, 0111, 1001, 1011, 1100, 1101.

Разобъем коды исходных импликант на группы, поместим их в таблицу. Далее применим закон склеивания к членам соседних групп, перебирая каждый член 1-й группы со всеми членами 2-й группы и т.д.

Можно все это сразу делать в таблице.

 

Данная функция	Результаты 1-го склеивания	Результаты 2-го склеивания
Коды	группы	Коды	группы	Коды	группы
	0-я	-	0-11	1-я	-011	-10-
	1-я	0100 *	-011		-100 *	-10-
	2-я	0011 *	010-		-101 *
		0101 *		2-я	0-11
		1001 *	01-1		1-01
		1100 *	-101	3-я	01-1
	3-я	0111 *	10-1		10-1
		1011 *	1-01	4-я	010- *
		1101 *	110-		110- *

 

Далее строится таблица меток, но в нее вписываются исходные и первичные импликанты в виде двоичных кодов. Обратите внимание, что первичные импликанты записаны в другом порядке (согласно их группам), поэтому таблица меток выглядит иначе, чем в примере 5.

 

-011		v					v
0-11		v				v
1-01				v				v
01-1			v			v
10-1				v			v
-10-	v		v		v			v

 

Обработка таблицы меток производится по методу Квайна.