Л.С. Тихомирова
Л.С. Тихомирова
МЕТОДЫ минимизации булевых функций
Прогресс во многих областях человеческой деятельности связан с решением проблем автоматизации процессов обработки и преобразования информации. Математическими носителями информации являются сигналы. Способ преобразования информации любой физической системой характеризуется законом функционирования системы. Удобно кодировать информацию (отвлекаясь от ее характера и смысла) конечным набором символов (букв). Законы функционирования системы описываются логическими функциями (булевыми функциями). Один и тот же закон можно реализовать функциями, имеющими различное число знаков, соединенных различными логическими операциями. Любая булева функция может быть записана в фиксированном виде (СДНФ или СКНФ), но эта запись не экономна. Проблема простейшего представления функции сводится к проблеме выбора базиса и проблеме наиболее экономного представления функции в этом базисе. Это и есть проблема минимизации функции. В настоящее время наибольшее распространение получил базис, состоящий из инверсии, конъюнкции и дизъюнкции (‾, Ù, Ú). Образующие его функции наиболее просты с точки зрения математических преобразований и технической реализации, кроме того, от них легко перейти в любой другой базис. Минимизация функций проводится обычно в классе ДНФ, но возможна и в КНФ. В основу положены два закона: Закон склеивания Закон поглощения Нормальная форма заданной функции (дизъюнктивной и конъюнктивной) называется минимальной, если количество букв, которое она содержит, будет не больше, чем в любой другой ее нормальной форме. Обратите внимание, что речь идет о минимальном числе букв, а не переменных. Например, Некоторые функции имеют несколько минимальных форм. Они могут быть найдены специальными способами, которым и посвящена данная разработка. С элементами математической логики можно познакомиться по методической разработке “Элементы теории множеств и математической логики” (Л.С. Тихомирова, И.Н. Иноземцева. Издание ИМИ, 1974 г.). Введем некоторые необходимые понятия. Рассмотрим функцию Если функция Другими словами, Функция Среди импликант данной функции Например:
(знак Простые импликанты представляют собою самые короткие произведения, входящие в данную функцию. Если какое-либо элементарное произведение входит в данную функцию, то при добавлении к нему любых сомножителей новое произведение также будет входить в эту функцию, т.к. оно обращается в нуль вместе с исходным произведением. Любая булева функция равна дизъюнкции всех своих простых импликант. Это представление функции называется сокращенной дизъюнктивной нормальной формой. Сокращенная форма характеризуется тем, что ее члены самые короткие, из нее уже нельзя исключать ни одной буквы, но можно выбросить некоторые импликанты. Если из сокращенной формы исключить все возможные члены, то получится тупиковая дизъюнктивная нормальная форма. Тупиковых форм у булевой функции может быть несколько. Тупиковая форма, содержащая наименьшее число членов, называется кратчайшей дизъюнктивной нормальной формой. Кратчайшая и тупиковые формы в общем случае не совпадают. Приведем схему упрощения формы булевой функции
|

 (или
(или  , где
, где  - произвольная булева функция,
- произвольная булева функция,  - отдельный знак).
- отдельный знак). (или
(или  , где
, где 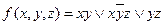 содержит 7 букв, но 3 переменных.
содержит 7 букв, но 3 переменных. . Каждое из слагаемых соответствует только одной единицы в таблице истинности данной функции. Говорят, что каждое слагаемое покрывает единицу функции, а в совокупности они покрывают данную функцию т.е. являются ее покрытием. Но заметим, что упростив функцию
. Каждое из слагаемых соответствует только одной единицы в таблице истинности данной функции. Говорят, что каждое слагаемое покрывает единицу функции, а в совокупности они покрывают данную функцию т.е. являются ее покрытием. Но заметим, что упростив функцию  , получим более простое покрытие. Оба представления соответствуют одной и той же таблице истинности функции, т.е. обращаются в 1 и 0 на одних и тех же наборах переменных
, получим более простое покрытие. Оба представления соответствуют одной и той же таблице истинности функции, т.е. обращаются в 1 и 0 на одних и тех же наборах переменных  . Если обратиться к отдельным слагаемым 2-го представления, нетрудно заметить, что
. Если обратиться к отдельным слагаемым 2-го представления, нетрудно заметить, что  - на (0, 0), (1, 0), совместно они покрывают единицами все единицы данной функции. Отметим, что оба слагаемых
- на (0, 0), (1, 0), совместно они покрывают единицами все единицы данной функции. Отметим, что оба слагаемых  обращаются одновременно в нуль на наборе (0, 1), т.е. там, где функция
обращаются одновременно в нуль на наборе (0, 1), т.е. там, где функция 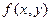 равна нулю.
равна нулю. равна нулю на тех же наборах переменных, на которых равна нулю данная функция
равна нулю на тех же наборах переменных, на которых равна нулю данная функция  , то говорят, что функция
, то говорят, что функция 
 - является простой импликантой
- является простой импликантой означает вхождение в
означает вхождение в  означает, что условия вхождения не выполняются).
означает, что условия вхождения не выполняются).



