Приложение. .
Приложение. Контрольная работа по теме: Тригонометрические функции. 10 класс. Вариант 1. 1. Найдите значение выражения: 1) 2. Сравните с нулём выражения: sin 1200, cos 1950, ctg 3590. Выберите правильную серию ответов: 1) + – – 2) – – + 3) + + – 4) + – + 3. Вычислите: 1) 12; 2) 4. Упростите выражение: 1) – cos2a; 2) cos2a; 3) sin2a; 4) – sin2a. 5. Упростите выражение: sina * cos a * ctg a – 1 1) 0; 2) cos2a; 3) – sin2a; 4) sin2a. 6. Упростите выражение: 1) sin a – cos a; 2) –2 ctg 2a; 3) tg 2a; 4) 0, 5 ctg 2a. 7. Вычислите: 2sin 150 * cos 150 1) 8. Вычислите: cos 1) 9. Представив 1050 как 600 + 450, вычислите sin 1050. 1) 10. Дано: sin a = – 1)
Контрольная работа по теме: Тригонометрические функции. 10 класс. Вариант 2.
 ; 4) 1, 5. ; 4) 1, 5.
1) + – + 2) – + + 3) – – + 4) – + –
 ; 2) - ; 2) -  ; 3) - ; 3) -  ; 4) ; 4)  . .
 ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  . .
 ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  . . 
Вариант 1. Найдите область определения функции 1) 2. Найдите область значений функции у = cos x +2 1) [-1; 1]; 2) [-2; 2]; 3) [0; 2]; 4) [1; 3]. 3. Проверьте функцию на четность у = х4+ cos x 1) четная; 2) нечетная; 3) ни четная, ни нечетная; 4) периодическая. 4. Найдите нули функции 1) 0; 2) 1; 3) 0; 1; 4) нет.
1) [-3; -2] U [2; 5]; 2) [-3; 5]; 3) [-2; 2]; 4) [2; 5]. 6. Найдите наименьший положительный период функции 1) π; 7. Найдите наименьшее значение функции у = х2 + 3х – 1 1) -1; 2) -3, 25; 3) -1, 5; 4) 1, 25. 8. Укажите график функции у = (х-1)2+4
1) 2) 3) 4) 9. Найдите промежутки, на которых у> 0
1) (-2; 2); 2) [-2; 0)U(2; 4); 3) [-2; -1) U (2; 4]; 4) [0; 3].
10. Дана функция f (x)= x3-2ax + 8. Известно, что f (1) = 5. Найдите f (-2). 1) 16; 2) 0; 3) 8; 4) -8. 11. Укажите функцию, которой соответствует данный график
Вариант 1. Найдите область определения функции и 1) 2. Найдите область значений функции у = sin x -2 1) [-1: 1]; 2) [-3: -1]; 3) (-2; 0); 4) [-2; 2]. 3. Проверьте функцию на четность: 1) четная; 2) нечетная; 3) ни четная, ни нечетная; 4) убывающая.
1) 3; 2) -3; 3) 0; 4) -5. 5. По графику некоторой функции у= f (x) найдите промежутки возрастания
1) [-2; 3]U [2; 4]; 2) [-3; 5]; 3) [0; 3]; 4) (-1; 2).
6. Найдите наименьший положительный период функции у = tg 4x 1) 2π; 7. Найдите наименьшее значение функции у = -х2 + 5х – 9 1) 8. Укажите график функции у = -2x-3
1) 2) 3) 4)
9. Найдите промежутки, на которых у< 0
3) (-3; -1); 4) [1; 4].
10. Дана функция f (x)= x3+5x -a. Известно, что f (2) = 15. Найдите f (-1). 1) -3; 2) -9; 3) -8; 4) 0. 11. Укажите функцию, которой соответствует данный график
3)
Контрольная работа по теме: Тригонометрические уравнения и неравенства. 10 класс. Вариант 1. Вычислите: arcsin ( 1) 2. Вычислите: arcos ( 1) 3. Решите уравнение: sin x - 1) 4. Решите уравнение: cos 2x=1 1) 5. Укажите уравнение, которому соответствует решение: 1) tg x = 1; 2) cos x = 0; 3) sin x = -1; 4) ctg x = 6. На каком из рисунков показано решение неравенства: cos x < 1) 2) 3) 4)
1) 8. Решите уравнение: 6sin2 x + sin x – 1 = 0 1) 9. Решите уравнение: 2sin2 x - 10. Решите систему:
Вариант 1. Вычислите: arcsin ( 1) 2. Вычислите: arcos ( 1) 3. Решите уравнение: sin x + 1) 4. Решите уравнение: ctg (x+ 1) 5. Укажите уравнение, которому соответствует решение: 1) ctg x = -1; 2) cos x = 0; 3) cos x = -1; 4) tg x = 1. 6. На каком из рисунков показано решение неравенства: sin x ≥
7. Решите неравенство: ctg x ≥ 1) 8. Решите уравнение: cos2 x - 4sin x + 3 = 0 1) 9. Решите уравнение:
10. Решите систему:
Вариант. 1. Найдите производную функции 1) 3) 2. Найдите значение производной функции 1) 1; 2) 0; 3) 0, 5; 4) -1. 3. Для какой функции найдена производная 1) 4. Найдите значение углового коэффициента касательной, проведенной к графику функции
1) -3; 2) 0; 3) 3; 4) 5.
5. Найдите
6. Напишите уравнение касательной к графику функции с абсциссой
1) у = - 3х – 3; 2) у = 8х+13; 3) у = - 8х – 3; 4) у = - 8х +13.
7. Найдите скорость и ускорение точки в момент времени 1)
9. По графику производной функции 1
убывания функции
10. Найдите наибольшее и наименьшее значение функции
11. Найдите производную функции
Вариант. 1. Найдите производную функции 1) 2. Найдите значение производной функции 1) 3. Для какой функции найдена производная 1)
1) у = - 9х – 6; 2) у = - 3х - 6; 3) у = 9х+16; 4) у = 9х - 6. 7. Найдите скорость и ускорение точки в момент времени 1)
функции
10. Укажите наибольшее и наименьшее значение функции 11. Вычислите производную функции
1 Вариант. 1. Найдите тангенс угла наклона касательной, проведенной к графику функции 1) -1, 5; 2) 3; 3) -3; 4) - 4, 5. 2. Решите неравенство:
1) [0; 1]U[4; +
3. Напишите уравнение касательной к графику функции в точке с абсциссой
1) у = – 12х + 17; 2) у = 12х – 17; 3) у = 19х – 38; 4) у = 12х+32.
4. Решите неравенство
1)
5. Найдите скорость и ускорение точки в момент времени t = 1cек., если она движется прямолинейно по закону 1)
6. Определите абсциссы точек, в которых угловой коэффициент касаcтельной к графику функции
1) 7. Решите неравенство 1)
8. Вычислите с помощью формул приближенные значения выражений:
а)
Вариант. 1. Найдите тангенс угла наклона касательной, проведенной к графику функции 1) -6; 2) 4; 3) 6; 4) -5. 2. Решите неравенство:
3. Напишите уравнение касательной к графику функции в точке с абсциссой
4. Решите неравенство
5. Найдите скорость и ускорение точки в момент времени t = 1 cек., если она движется прямолинейно по закону
6. Определите абсциссы точек, в которых угловой коэффициент касательной к графику функции
7. Решите неравенство
8. Вычислите с помощью формул приближенные значения выражений:
|


 ; 2)
; 2)  ; 3)
; 3)  ; 4) 0.
; 4) 0.
 ; 3) 6; 4) 0.
; 3) 6; 4) 0.

 ; 2)
; 2)  ; 3)
; 3)  .
.
 ; 2)
; 2)  ; 3)
; 3)  ; 4) 0.
; 4) 0. где
где  . Найдите tg 2a
. Найдите tg 2a ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.




 1)
1) 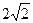 ; 2)
; 2)  ; 3)
; 3)  ; 4) 0.
; 4) 0. 1500 1)
1500 1)  ; 2)
; 2) 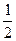 ; 3)
; 3)  ; 4)
; 4)  .
. где
где  . Найдите ctg 2a
. Найдите ctg 2a 

 2)
2)  3)
3)  4)
4)  .
.
 5. По графику некоторой функции у= f (x) найдите промежутки возрастания
5. По графику некоторой функции у= f (x) найдите промежутки возрастания





 1)
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
 2)
2)  3)
3)  4)
4)  .
.
 4. Найдите нули функции
4. Найдите нули функции 
 ; 3) 0, 5 π; 4) 4 π.
; 3) 0, 5 π; 4) 4 π. ; 2) -9; 3) 1, 5; 4) 9, 75.
; 2) -9; 3) 1, 5; 4) 9, 75.



 1) (-1; 3); 2) [-3; 1]U[4; 5];
1) (-1; 3); 2) [-3; 1]U[4; 5]; 1)
1)  ; 2)
; 2)  ;
; ; 4)
; 4)  .
. ) + 2arctg(-1)
) + 2arctg(-1) ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. ) + 2arcctg(
) + 2arcctg( ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. 2)
2)  ; 3)
; 3)  4)
4) 
 2)
2)  3)
3) 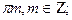 4)
4) 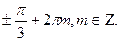
 :
: .
.
 2)
2)  3)
3)  4)
4) 
 3) нет корней; 4)
3) нет корней; 4)  .
.
 ; 2)
; 2)  ; 3)
; 3)  ) + arcctg (
) + arcctg ( )
) ; 3)
; 3)  ; 4)-
; 4)-  ; 3)
; 3)  4)
4) 
 2)
2)  3)
3)  4)
4) 
 :
: 1) 2) 3) 4)
1) 2) 3) 4) 2)
2)  3)
3)  4)
4) 
 2)
2)  3) нет корней; 4)
3) нет корней; 4)  .
.

 2)
2) 
 4)
4) 
 в точке
в точке 

 2)
2)  3)
3)  4)
4) 
 в точке с абсциссой
в точке с абсциссой 
 , если
, если  sin
sin  1)
1)  2)
2)  3)
3)  4) 0.
4) 0. в точке
в точке
 c., если она движется прямолинейно по закону
c., если она движется прямолинейно по закону  (координата
(координата  измеряется метрах).
измеряется метрах).
 2)
2)  3)
3)  4)
4) 
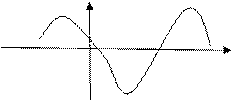 8. Определите точку максимума функции
8. Определите точку максимума функции 





 на промежутке
на промежутке 


 2)
2)  3)
3)  4)
4) 
 в точке
в точке 
 2)
2)  3)
3)  4)
4) 
 sin
sin  2)
2)  3)
3)  4)
4) 





 в точке с абсциссой
в точке с абсциссой  , если
, если  . 1) 0; 2) -1; 3)
. 1) 0; 2) -1; 3)  4) -
4) -  . 6. Напишите уравнение касательной к графику функции
. 6. Напишите уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  .
. cек., если она движется прямолинейно по закону
cек., если она движется прямолинейно по закону  (координата
(координата  измеряется в метрах).
измеряется в метрах). 2)
2)  3)
3)  4)
4) 
 8. Определите минимум функции
8. Определите минимум функции  у
у


 9. По графику производной функции
9. По графику производной функции  укажите длину промежутка возрастания 0 1 х
укажите длину промежутка возрастания 0 1 х на данном промежутке
на данном промежутке  .
. , если
, если 
 в точке
в точке 

 ; 2) (
; 2) ( ; 0)U(1; 4); 3)
; 0)U(1; 4); 3)  4) (0; 1)U(4;
4) (0; 1)U(4;  .
.

 методом интервалов.
методом интервалов. 2)
2)  3)
3)  4)
4) 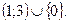
 (координата
(координата  2)
2)  ; 3)
; 3)  ; 4)
; 4)  .
. sin
sin  равен 2.
равен 2. n, n
n, n 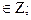 2)
2)  3)
3)  4)
4)  sin2.
sin2. где
где 
 ; 2)
; 2)  3)
3)  ; 4)
; 4) 
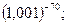 б)
б) 





 методом интервалов.
методом интервалов.


 sin
sin  равен 2.
равен 2.
 где
где 






