Тема 1.2 Системы автоматического регулирования
1. Состав системы автоматического регулирования 2. Классификация систем регулирования производством 3. Типовые динамические звенья САР и их характеристики 4. Устойчивость систем автоматического регулирования.
1. Система автоматического регулирования (САР) – совокупность объекта управления и автоматического регулятора, взаимодействующих между собой в соответствии с алгоритмом управления. Автоматическим регулированием называют поддержание значений физических величин на определенном уровне или изменение их по требуемому закону без непосредственного участия человека. Технические устройства, в которых процессы подлежат автоматическому регулированию, называют объектами регулирования. Физические величины, подлежащие регулированию, называют регулируемыми величинами. Внешние воздействия, вызывающие отклонение регулируемой величины от ее заданного значения, называют возмущающими воздействиями. Технические устройства, предназначенные для автоматического регулирования различных величин в объектах, называют автоматическими регуляторами. Система автоматического регулирования состоит из двух основных частей - объекта регулирования и автоматического регулятора. САР представляет собой сложные комплексы взаимодействующих технических средств, узлов и элементов, работа которых основана на различных физических принципах (электрических, механических, гидравлических и др.). Они разнообразны по конструктивному исполнению и техническим характеристикам. Однако в теории автоматического регулирования основное внимание уделяется не техническим свойствам отдельных элементов, а их функциональным преобразованиям и характеру связей между ними. Наглядное представление об этом дают функциональные схемы систем автоматического регулирования. Функциональные схемы отражают взаимодействие устройств, элементов систем автоматического регулирования в процессе их работы. Графически отдельные устройства систем автоматического регулирования изображают в виде прямоугольников, а существующие между ними связи - стрелками, соответствующими направлению прохождения сигнала. Внутреннее содержание каждого устройства не конкретизируется, а функциональное назначение шифруется буквенными символами. Типовая (или обобщенная) функциональная схема системы автоматического регулирования представлена на рисунке 8. На объект регулирования ОР, находящийся под влиянием внешнего возмущающего воздействия F, поступает управляющее воздействие хр, которое является выходной величиной автоматического регулятора (АР), представляющего собой совокупность элементов. В автоматический регулятор по цепи главной обратной связи (ОСГ) поступает регулируемая величина хвых. Входная величина хвх с задатчика З поступает на элемент сравнения (ЭС). Сигнал ошибки, представляющий собой разность входной величины хвх и сигнала главной обратной связи хос (Δ х=хвх-хос) поступает на усилитель У, где усиливается в К раз и воздействует на исполнительный элемент (ИЭ), выходной сигнал хр которого является регулирующим воздействием автоматического регулятора. Элемент местной обратной связи (ОСМ) вводится в систему автоматического регулирования для улучшения ее динамических свойств.
Рисунок 8 - Функциональная схема систем автоматического регулирования
2. Классификация систем. Вследствие большого разнообразия используемых в технике систем автоматического регулирования, различающихся функциональными возможностями, принципами построения и формой конструктивной реализации, невозможно дать единую классификацию систем автоматического регулирования. Рассмотрим наиболее характерные классификационные признаки. 1) Наличие в системах явно выраженной обратной связи: разомкнутые и замкнутые. Замкнутые системы содержат цепь главной обратной связи ОСГ, в разомкнутых системах она отсутствует. Системы, работающие по разомкнутому циклу, используют только в качестве составной части более сложных систем автоматического регулирования. Под главной обратной связью понимают подачу части энергии с выхода системы на ее вход. Главная обратная связь (ОСГ) служит для сравнения действительного закона изменения регулируемого параметра с требуемым. Помимо главной обратной связи в системе предусмотрена местная обратная связь, которая охватывает один или несколько элементов основной цепи. Обратную связь называют положительной, если ее выходной сигнал суммируется с основным сигналом, и отрицательной, если этот сигнал вычитается из основного сигнала. 2) Закон изменения регулируемой величины в системах автоматического регулирования: системы стабилизации, программного регулирования и следящие. Системы стабилизации предназначены для поддержания постоянного значения регулируемой величины. В этих системах задающее воздействие не изменяется во времени. Системы программного регулирования предназначены для изменения регулируемой величины по известному закону в функции времени или какой-либо другой величины. Задающее воздействие называют программой регулирования. Следящие системы предназначены для изменения регулируемой величины по заранее неизвестному закону. Задающее воздействие представляет собой случайную функцию времени. 3) Способность САР поддерживать с определенной степенью точности значение регулируемой величины: статические и астатические. Статической системой автоматического регулирования называют такую систему, в которой принципиально невозможно поддерживать одно и то же значение регулируемого параметра при условии, что задающее воздействие системы остается неизменным. Остаточную ошибку в такой системе называют статизмом. Астатической системой автоматического регулирования называют такую систему, в которой в установившемся режиме регулируемый параметр принимает всегда одно и то же значение и не зависит от значения возмущающего воздействия на объект регулирования. В астатической системе статизм всегда равен нулю. 4) Функциональная связь между входными и выходными величинами элементов, входящих в состав системы автоматического регулирования: непрерывные и дискретные. Непрерывной системой автоматического регулирования называют систему, в которой непрерывному изменению входных величин элементов соответствует непрерывное изменение выходных величин этих эле-ментов. Дискретной системой автоматического регулирования называют систему, в которой непрерывному изменению входной величины хотя бы одного элемента, входящего в состав системы, соответствует дискретное изменение выходной величины этого элемента. При изучении динамических свойств систем целесообразно рассматривать отдельные ее элементы только с точки зрения их динамических свойств независимо от функциональных преобразований и конструктивных форм исполнения. Одинаковыми динамическими свойствами могут обладать различные элементы независимо от их физической природы. По этому признаку в цепях регулирования принято выделять отдельные элементы или группы элементов, которые называют динамическими звеньями. Динамическим звеном называют часть системы автоматического регулирования, переходный процесс которой описывается дифференциальным уравнением определенного вида. Динамическим звеном может быть элемент, совокупность элементов и вся система автоматического регулирования в целом. Графически динамическое звено изображается в виде прямоугольника, внутри которого вписывается выражение передаточной функции W (р), а направление прохождения информации изображается стрелками. Входной и выходной сигналы в динамическом звене могут иметь различную физическую природу. В теории автоматического регулирования можно выделить следующие типовые динамические звенья - безынерционное (пропорциональное), апериодическое (инерционное), дифференцирующее, интегрирующее, колебательное. Характеристики динамических звеньев Зависимость выходной величины звена от входной в установившемся режиме называют статической характеристикой. Установившийся режим — это такой режим, при котором входная и выходная величины остаются постоянными во времени. Статическую характеристику обычно изображают графически. Ее значения можно получать экспериментально или расчетным путем. Системы автоматического регулирования, как правило, работают в неустановившемся, переходном режиме. Такой режим работы является следствием воздействия на систему непрерывно и случайно изменяющихся внешних возмущающих факторов, приводящих к непрерывному изменению входной и выходной величины во всех ее звеньях. Поэтому одной из важных задач является изучение поведения динамических звеньев в переходных режимах. Динамической характеристикой звена называют зависимость выходной величины от входной в переходном процессе. Физическая задача определения выходной величины звена при изменяющемся входном сигнале сводится к решению дифференциального уравнения того или иного вида, описывающего протекание переходных процессов в звене. Дифференциальные уравнения движения динамического звена. В линейных системах автоматического регулирования протекающие процессы описываются линейными дифференциальными уравнениями, решение которых значительно упрощается с использованием методов операционного исчисления. Решение дифференциального уравнения методом операционного исчисления осуществляется в следующие три этапа; 1) переход от оригиналов к изображениям, т. е. переход от дифференциального уравнения к алгебраическому; 2) отыскание из полученного алгебраического уравнения неизвестной функции Y (р), т. е. решение алгебраического уравнения; 3) переход от найденного изображения Y (р) к оригиналу неизвестной функции. Дифференциальные уравнения движения звеньев имеют следующий вид: - безинерционное звено: - апериодическое: - дифференцирующее: - интегрирующее: - колебательное: где
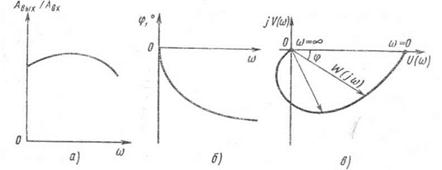
Передаточная функция. Передаточной функцией звена называется отношение изображения выходной величины звена к изображению входной величины при нулевых начальных условиях. Обозначим через W (р) передаточную функцию, а через X (р) и Y (р) - соответственно изображения входной и выходной величин, тогда: W(p) = Y (р)/Х (р) [1.18] Переходная характеристика. Переходной характеристикой (переходным процессом) динамического звена называют зависимость выходной величины от времени при подаче на вход звена ступенчатого сигнала единичной амплитуды. Следовательно, переходная характеристика отображает реакцию звена на единичный ступенчатый сигнал. Частотные характеристики звеньев. Если на вход динамического звена поступает сигнал синусоидальной формы определенной частоты, то выходной сигнал имеет те же синусоидальную форму и частоту, но другие амплитуду и фазу. В связи с этим различают амплитудно-частотные и фазово-частотные характеристики звеньев. Амплитудно-частотная характеристика выражает отношение амплитуды колебаний на выходе звена к амплитуде колебаний на его входе в зависимости от частоты выходного сигнала (Рисунок 9, а) А (ω) = Авых/Авх = f (ω), [1.19] где Авых - амплитуда выходного сигнала; Авх - амплитуда входного сигнала; ω - угловая частота.
Рисунок 9 - Частотные характеристик звеньев: а- амплитудно-частотная; б - фазово-частотная; в – амплитудно-фазовая Фазово-частотная характеристика выражает зависимость разности фаз между входными и выходными колебаниями звена от частоты входного сигнала (Рисунок 9, б ): φ = f(ω), [1.20] где φ - фазовый угол. Опережению фазы соответствует φ > 0, а отставанию φ < 0. В теории автоматического регулирования используют комплексную амплитудно-фазовую характеристику (Рисунок 9, в), в которой дают соотношения между амплитудами выходного и входного сигналов и сдвигом фаз при изменении частоты колебаний входного сигнала от 0до ∞: W (jω) = Авых/Авх= Авыхej(ω t+φ )/Авхejω t= Авыхejφ /Авх= А(ω)ejφ (ω), [1.21] где Авыхej(ω t+φ ); Авхejω t - соответственно выходной и входной сигналы в символической форме записи. Существует показательная форма записи: W (jω) = А(ω)еjφ (ω) [1.22] Величина А (ω) - изменение отношения амплитуд выходного сигнала к входному, а φ (ω) - изменение фазы колебаний на выходе звена относительно колебаний на входе, происходящих с изменением частоты входного сигнала. Логарифмической амплитудно-частотной характеристикой (ЛАЧХ) L (ω) называют зависимость модуля частотной характеристики от частоты, представленную в логарифмическом масштабе. Логарифмической фазово-частотной характеристикой (ЛФЧХ) называют зависимость аргумента частотной характеристики от логарифма частоты. Для построения ЛАЧХ от выражения амплитудно-фазовой характеристики вида W (jω) = А(ω)еjφ (ω) переходят к выражению L (ω) = 20 lg |W (ω)|= 20 lg A (ω), [1.23] где L (ω) — в децибелах. При построении ЛФЧХ по оси ординат откладывают углы в градусах или радианах, по оси абсцисс - частоту со в логарифмическом масштабе в декадах. 4. Необходимым условием работоспособности системы автоматического регулирования является ее устойчивость. Под устойчивостью понимают свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов, после прекращения действия этих факторов. На практике для определения устойчивости САР используют критерии устойчивости, т.е. правила, с помощью которых можно определить, устойчива система или не, не прибегая к решению дифференциальных уравнений. Алгебраический критерий (Рауса-Гурвица) позволяет судить об устойчивости замкнутой системы по коэффициентам ее характеристического уровня, которым является знаменатель передаточной функции. Необходимые и достаточные условия устойчивости определяются различными соотношениями коэффициентов в зависимости от порядка системы. Критерий устойчивости Михайлова основан на связи характера переходного процесса системы с амплитудой и фазой вынужденных колебаний, устанавливающих в системе при синусоидальном воздействии. Анализ устойчивости системы этим методом сводится к построению по характеристическому многочлену замкнутой системы (знаменатель передаточной функции) комплексной частотной функции, по виду которой можно судить об устойчивости. Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы САР по амплитудно-фазовой характеристике. Замкнутая система будет устойчива в том случае, если устойчива замкнутая система и ее амлитудно-фазовая характеристика не охватывает точку с координатами (-1, j0), называемую критической. При отсутствии местных обратных связей разомкнутая система всегда устойчива, если состоит из устойчивых звеньев. При наличии местных обратных связей система может оказаться неустойчивой в разомкнутом состоянии. Устойчивость по логарифмическим частотным характеристикам определяют с использованием критерия устойчивости Найквиста. Замкнутая система устойчива, если на частоте ω, для которой φ =-π, ордината ЛАЧХ разомкнутой системы отрицательна, т.е. L(ω)< 0. Если разомкнутая система устойчива, а ЛАЧХ пересекает линию -π в нескольких точках, то замкнутая система будет устойчивой, когда L(ω)< 0 при φ =-π для конечной правой из точек пересечения. Для определения устойчивости системы используют приближенную ЛАЧХ, представляющую собой ломаную линию, отдельные участки которой имеют определенный наклон.
|

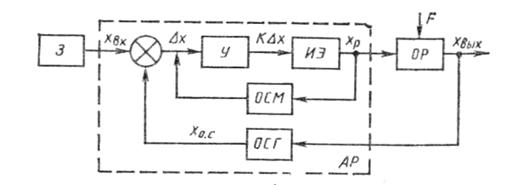
 [1.13]
[1.13] [1.14]
[1.14] [1.15]
[1.15] [1.16]
[1.16] , [1.17]
, [1.17]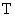 – постоянная времени звена,
– постоянная времени звена, - коэффициент демпфирования.
- коэффициент демпфирования.