Тема 7. Свойства водных растворов неэлектролитов
Пример 1. Раствор, содержащий 1, 22 г бензойной кислоты C6H5COOH в 100 г сероуглерода кипит при 46, 5290С. Температура кипения сероуглерода 46, 30С. Вычислите эбуллиоскопическую константу сероуглерода. Решение. 1. Рассчитываем повышение температуры кипения
2. С использованием атомных масс элементов рассчитываем молярную массу бензойной кислоты
3. По формуле находим эбуллиоскопическую константу
Пример 2. Раствор, содержащий 22, 04 г глицерина в 1600 г воды, кристаллизуется при -0, 2790С. Вычислите молярную массу глицерина. Решение. 1. Рассчитываем понижение температуры замерзания. Известно, что температура кристаллизации чистой воды равна 00С, следовательно, понижение температуры кристаллизации
2. Используя формулу выражаем и рассчитываем молярную массу глицерина
Пример 3. Вычислите массовую долю водного раствора мочевины (NH2)2CO, зная, что температура кристаллизации этого раствора равна «-0, 930С». Решение. 1. Рассчитываем понижение температуры замерзания. Известно, что температура кристаллизации чистой воды равна 00С, следовательно, понижение температуры кристаллизации
2. С использованием атомных масс элементов рассчитываем молярную массу мочевины
3. Находим массу растворенного вещества, приходящуюся на 1000 г воды, по формуле ()
4. Общая масса раствора рассчитывается суммированием массы растворителя (1000 г) и массы растворенного вещества (30г)
5. Рассчитываем массовую долю мочевины по формуле
|







 .
.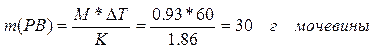 .
.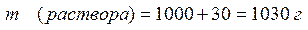 .
.