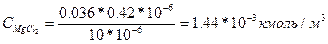Тема 11. Химическая кинетика и равновесие
Кинетика — учение о скорости различных процессов, в том числе химических реакций. Критерием принципиальной осуществимости реакций является неравенство DGР, T < 0. Но это неравенство не является полной гарантией фактического течения процесса в данных условиях, не является достаточным для оценки кинетических возможностей реакции. Так, Н2(г) + 72 О2(г) = Н2О(г) (I) 2А1(к) + 3J2(к) = 2АП3(к) (II) Однако эти реакции при стандартных условиях идут только в присутствии катализатора (платина для первой и вода для второй). Катализатор как бы снимает кинетический «тормоз» и проявляется термодинамическая природа вещества. Скорость химических реакций зависит от многих факторов, основные из которых — концентрация (давление) реагентов, температура и действие катализатора. Эти же факторы определяют и достижение равновесия в реагирующей системе. Пример 1. Во сколько раз изменится скорость прямой и обратной реакции в системе 2SO2(r) + О2(г) если объем газовой смеси уменьшится в три раза? В какую сторону сместится равновесие системы? Решение. Обозначим концентрации реагирующих веществ: [SO2] = а, [О2] = b, [SO3] = с. Согласно закону действующих масс, скорости прямой и обратной реакций до изменения объема равны vnp = Ka2b, vo6p = K1c2. После уменьшения объема гомогенной системы в три раза концентрация каждого из реагирующих веществ увеличится в три раза: [SO2] = За, [О2] = 3b; [SO3] = Зс. При новых концентрациях скорости v'np прямой и обратной реакций: v'np = K(3ф)2 (3b) = 27 Ka2b; vo6p = K1(Зс)2 = 9K1c2. Отсюда
Следовательно, скорость прямой реакции увеличилась в 27 раз, а обратной — только в девять раз. Равновесие системы сместилось в сторону образования SO3. Пример 2. Вычислите, во сколько раз увеличится скорость реакции, протекающей в газовой фазе, при повышении температуры от 30 до 70° С, если температурный коэффициент реакции равен 2. Решение. Зависимость скорости химической реакции от температуры определяется эмпирическим правилом Вант-Гоффа по формуле
Следовательно, скорость реакции Пример 3. Константа равновесия гомогенной системы| СО(г) + Н2О(г) при 850° С равна 1. Вычислите концентрации всех веществ при равновесии, если исходные концентрации: [СО]ИСХ = 3 моль/л, [Н2О]ИСХ = 2 моль/л. Решение. При равновесии скорости прямой и обратной реакций равны, а отношение констант этих скоростей постоянно и называется константой равновесия данной систем vnp = K1[CO][H2O]; vo6p = K2[CO2][H2];
В условии задачи даны исходные концентрации, тогда как в выражение Кр входят только равновесные концентрации всех веществ системы. Предположим, что к моменту равновесия концентрация [СО2]Р = х моль/л. Согласно уравнению системы число молей образовавшегося водорода при этом будет также х моль/л. По столько же молей (х моль/л) СО и Н2О расходуется для образования по х молей СО2 и Н2. Следовательно, равновесные концентрации всех четырех веществ (моль/л): [СО2]Р = [Н2]р = х; [СО]Р = (3 - х); [Н2О]Р = (2-х). Зная константу равновесия, находим значение х, а затем исходные концентрации всех веществ:
Таким образом, искомые равновесные концентрации: [СО2]Р = 1, 2 моль/л; [Н2]р = 1, 2 моль/л; [СО]Р= 3 - 1, 2 = 1, 8 моль/л; [Н2О]Р = 2- 1, 2 = 0, 8 моль/л. Пример 4. Эндотермическая реакция разложения пентахлорида фосфора протекает по уравнению РС15(г) Как надо изменить: а) температуру; б) давление; в) концентрацию, чтобы сместить равновесие в сторону прямой реакции — разложения РС15? Решение. Смещением или сдвигом химического равновесия называют изменение равновесных концентраций реагирующих веществ в результате изменения одного из условий реакции. Направление, в котором сместилось равновесие, определяется по принципу Ле Шателье: а) так как реакция разложения РС15 эндотермическая ( б) так как в данной системе разложение РС15 ведет к увеличению объема (из одной молекулы газа образуются две газообразные молекулы), то для смещения равновесия в сторону прямой реакции надо уменьшить давление; в) смещения равновесия в указанном направлении можно достигнуть как увеличением концентрации РСl5, так и уменьшением концентрации РСl3 или С12. Тема 12 Дисперсные системы (коллоидные растворы) Пример 1. Массовая концентрация пыли в воздухе рабочих зон помещений составляет 4, 2 мг/ м3. Определить численную концентрацию пыли, если средний диаметр частиц составляет 3, 7 мкм, а их плотность -1, 1 103кг/м3. Решение: учитывая, что V=(4/3) π r3 найдем vч = v м / (V p) = 3, 42 10-6/4 3, 14 (1, 85 10-6)3 1, 1 103=1, 44 108 м3. В 1 м3 воздуха содержится 144 млн. частиц. Пример 2. Вычислить степень адсорбции фенола на поверхности капель эмульгированного масла по экспериментальным данным в зависимости поверхностного натяжения водного фенола от его концентрации: σ ·103, Дж/м2 67, 88 60, 10 51, 58 44, 97 Решение: Согласно уравнению Гиббса Где величина dσ /dC может быть определена как тангенс угла наклона касательной кривой dσ =f(C) в точке где С=0. Строим кривую dσ =f(C). Тангенс угла наклона касательной равен 0, 0967. Вычисляем:
Пример 3. Для 0, 1%-ного раствора эфиров сахарозы, поверхностное натяжение которого составляет 30 мДж/м2, определить равновесную работу когезии и адгезии, если краевой угол смачивания к твердой поверхности равен 150. Решение. По уравнению определяем работу когезии:
Wk=2σ ж-г=2·3=60 мДж/м2, а равновесную работу адгезии по уравнению: Wа=σ ж-г(1+cos θ)=30(1+cos15) =59 мДж/м2. Пример 4. Как изменится порог коагуляции золя As2S, если для коагуляции потребуется 1, 2·10-6 м3 раствора NaCl концентрацией 0, 5 кмоль/м3? Определите порог коагуляции под действием раствора MgCl2, 0, 036 кмоль/м3, (его потребуется 0, 4·10-6м3 на 10·10-6 м3 золя) и раствора АlCl3, концентрацией 0, 01 кмоль/м3(его потребуется 0, 1·106м3 на 10·10-6м3 золя). По уравнению
|

 Н2О(г) = -228, 59 кДж/моль, а
Н2О(г) = -228, 59 кДж/моль, а  2SO3(г)
2SO3(г)



 при 70 С больше скорости реакции
при 70 С больше скорости реакции  при 30 С в 16 раз.
при 30 С в 16 раз.
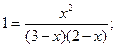


 = +92, 59 кДж.
= +92, 59 кДж.
 .
. , найдем
, найдем