Расчет погрешностей при косвенных измерениях
В большинстве случаев конечной целью лабораторной работы является вычисление искомой величины с помощью некоторой формулы, в которую входят величины, измеряемые прямым путем. Такие измерения называются косвенными. В качестве примера приведем формулу плотности твердого тела цилиндрической формы
где r – плотность тела, m – масса тела, d – диаметр цилиндра, h – его высота. Зависимость (П.5) в общем виде можно представить следующим образом:
где Y – косвенно измеряемая величина, в формуле (П.5) это плотность r; X 1, X 2, ..., Xn – прямо измеряемые величины, в формуле (П.5) это m, d, и h. Результат косвенного измерения не может быть точным, поскольку результаты прямых измерений величин X 1, X2, ..., Xn всегда содержат в себе погрешность. Поэтому при косвенных измерениях, как и при прямых, необходимо оценить доверительный интервал (абсолютную погрешность)полученного значения DY и относительную погрешность e. При расчете погрешностей в случае косвенных измерений удобно придерживаться такой последовательности действий: 1) получить средние значения каждой прямо измеряемой величины á X1 ñ, á X2 ñ, …, á Xn ñ; 2) получить среднее значение косвенно измеряемой величины á Y ñ, подставив вформулу (П.6) средние значения прямо измеряемых величин; 3) провести оценки абсолютных погрешностей прямо измеряемых величин DX 1, DX 2,..., DXn, воспользовавшись формулами (П.2) и (П.3); 4) основываясь на явном виде функции (П.6), получить формулу для расчета абсолютной погрешности косвенно измеряемой величины DY и рассчитать ее; 5) рассчитать относительную погрешность измерения 6) записать результат измерения с учетом погрешности. Ниже без вывода приводится формула, позволяющая получить формулы для расчета абсолютной погрешности, если известен явный вид функции (П.6):
где ¶Y¤¶ X1 и т. д. – частные производные от Y по всем прямо измеряемым величинам X 1, X 2, …, X n (когда берется частная производная, например по X 1, то все остальные величины Xi в формуле считаются постоянными), D Xi – абсолютные погрешности прямо измеряемых величин, вычисленные согласно (П.3). Рассчитав DY, находят относительную погрешность Однако если функция (П.6) является одночленом, то намного легче сначала рассчитать относительную погрешность, а затем уже абсолютную. Действительно, разделив обе части равенства (П.7) на Y, получим
Но так как
Теперь, зная относительную погрешность, определяют абсолютную В качестве примера получим формулу для расчета погрешности плотности вещества, определяемой по формуле (П.5). Поскольку (П.5) является одночленом, то, как сказано выше, проще сначала рассчитать относительную погрешность измерения по (П.8). В (П.8) под корнем имеем сумму квадратов частных производных от логарифма измеряемой величины, поэтому сначала найдем натуральный логарифм r: ln r = ln 4 + ln m – ln p –2 ln d – ln h, а потом уже воспользуемся формулой (П.8) и получим, что
Как видно, в (П.9) используются средние значения прямо измеряемых величин и их абсолютные погрешности, рассчитанные методом прямых измерений по (П.3). Погрешность, вносимую числом p, не учитывают, поскольку ее значение всегда можно взять с точностью, превышающей точность измерения всех других величин. Рассчитав e, находим Если косвенные измерения являются независимыми (условия каждого последующего эксперимента отличаются от условий предыдущего), то значения величины Y вычисляются для каждого отдельного эксперимента. Произведя n опытов, получают n значений Yi. Далее, принимая каждое из значений Yi (где i – номер опыта) за результат прямого измерения, вычисляют á Y ñ и D Y по формулам (П.1) и (П.2) соответственно. Окончательный результат как прямых, так и косвенных измерений должен выглядеть так:
где m – показатель степени, u – единицы измерения величины Y.
|

 , (П.5)
, (П.5) , (П.6)
, (П.6)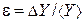 ;
; , (П.7)
, (П.7) .
. .
. , то можно записать
, то можно записать . (П.8)
. (П.8) .
. . (П.9)
. (П.9) .
.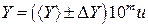 , (П.10)
, (П.10)


