ИССЛЕДОВАНИЕ ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
(вариант I – постоянным остается момент инерции) Цель работы: 1) показать, что при неизменном моменте инерции маятника Обербека отношение момента силы к угловому ускорению Приборы и принадлежности: маятник Обербека, набор грузов, секундомер, штангенциркуль, масштабная линейка. Описание установки и метода измерений
Основной закон динамики вращательного движения в данной работе удобно записать в виде 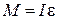 , (1.1) , (1.1)
где М – модуль результирующего момента сил, действующего на маятник, I – момент инерции маятника, Из (1.1) следует, что при неизменном моменте инерции угловое ускорение маятника должно изменяться пропорционально результирующему моменту сил. Это значит, во сколько раз изменится момент сил, во столько же раз должно измениться угловое ускорение, т. е. при неизменном моменте инерции
Проверка соотношений (1.2) и является целью данной работы. Результирующий момент сил представляет собой сумму двух моментов: момента Силу натяжения нити
В скалярной форме уравнение (1.3) имеет вид
откуда Так как плечо силы натяжения равно радиусу шкива R, то ее момент
Ускорение груза можно найти с помощью уравнения равноускоренного движения
где h – высота падения груза, Для определения момента силы трения
Моменты
Если окажется, что
Угловое ускорение маятника Обербека, соответствующее данному вращающему моменту, находят, руководствуясь следующими соображениями. Если нить, на которой подвешен груз m, считать нерастяжимой, то все точки нити и любая точка поверхности шкива имеют то же тангенциальное ускорение, что и груз, следовательно, угловое ускорение маятника
|

 остается постоянным; 2) найти момент инерции маятника.
остается постоянным; 2) найти момент инерции маятника.
 Маятник Обербека (рис. 1.1), с помощью которого производится исследование, состоит из шкива радиуса R, закреплённого на оси О, двух стержней Д, расположенных под углом 90˚ друг к другу, и четырёх одинаковых цилиндрических грузов С, которые можно перемещать вдоль стержней и закреплять на разных расстояниях от оси, а также кольца А. Грузы закрепляются симметрично, так, чтобы центр масс маятника совпадал с осью его вращения. Прибор приводится в движение с помощью груза В массой
Маятник Обербека (рис. 1.1), с помощью которого производится исследование, состоит из шкива радиуса R, закреплённого на оси О, двух стержней Д, расположенных под углом 90˚ друг к другу, и четырёх одинаковых цилиндрических грузов С, которые можно перемещать вдоль стержней и закреплять на разных расстояниях от оси, а также кольца А. Грузы закрепляются симметрично, так, чтобы центр масс маятника совпадал с осью его вращения. Прибор приводится в движение с помощью груза В массой 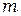 , прикреплённого к концу шнура, навитого на шкив.
, прикреплённого к концу шнура, навитого на шкив. – его угловое ускорение.
– его угловое ускорение. ,
,  ,
, 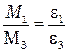 . (1.2)
. (1.2) , создаваемого силой натяжения нити
, создаваемого силой натяжения нити  , и момента силы трения в подшипниках
, и момента силы трения в подшипниках  .
. :
: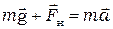 . (1.3)
. (1.3) ,
, . (1.4)
. (1.4) . (1.5)
. (1.5) , откуда
, откуда  , (1.6)
, (1.6) – время падения.
– время падения.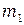 от 10 до 50 г. К нити поочередно прикрепляют гирьки и подбирают такую, при которой вращение маятника оказывается равномерным (для того, чтобы маятник начал вращаться, его надо подтолкнуть). Равномерное вращение указывает на то, что момент, созданный гирькой массой
от 10 до 50 г. К нити поочередно прикрепляют гирьки и подбирают такую, при которой вращение маятника оказывается равномерным (для того, чтобы маятник начал вращаться, его надо подтолкнуть). Равномерное вращение указывает на то, что момент, созданный гирькой массой  .
. имеют противоположные направления, поэтому модуль результирующего момента сил М, действующего на маятник, равен
имеют противоположные направления, поэтому модуль результирующего момента сил М, действующего на маятник, равен . (1.7)
. (1.7) < <
< < 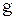 , то ускорением
, то ускорением  . (1.8)
. (1.8) . (1.9)
. (1.9)


