Описание установки и метода измерений. Маховое колесо М и шкив радиуса R насажены на единую ось О (рис
Маховое колесо М и шкив радиуса R насажены на единую ось О (рис. 1.2). На шкив навит шнурок, к которому прикреплён груз массой
где С помощью уравнения (2.1) можно экспериментально определить момент инерции махового колеса, если известны остальные величины:
где
откуда Подставив (2.3) в (2.2), получим формулу для расчета работы силы трения при движении груза вниз
На груз действуют постоянные силы, поэтому его движение является равноускоренным и описывается уравнениями
Исключив из этих уравнений ускорение, получим выражение для линейной скорости груза в нижней точке
Нить, на которой подвешен груз, практически нерастяжима, следовательно, линейная скорость точек обода шкива равна скорости груза. И угловую скорость махового колеса можно получить, используя соотношение между линейной и угловой скоростями (Т.5)
где t – время падения груза с высоты h 1. Подставив выражение (2.4), а также выражения (2.5) и (2.6) в (2.1), получим формулу для вычисления момента инерции махового колеса в данной работе
|

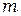 . Грузу сообщают потенциальную энергию, подняв его на высоту
. Грузу сообщают потенциальную энергию, подняв его на высоту 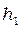 по отношению к некоторому уровню, высота которого принята за ноль. При падении груза его потенциальная энергия
по отношению к некоторому уровню, высота которого принята за ноль. При падении груза его потенциальная энергия 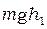 переходит в кинетическую энергию поступательного движения груза
переходит в кинетическую энергию поступательного движения груза  и кинетическую энергию вращательного движения маховика
и кинетическую энергию вращательного движения маховика  , а также расходуется на преодоление сил трения в подшипнике. Таким образом, закон сохранения механической энергии для данной системы имеет вид
, а также расходуется на преодоление сил трения в подшипнике. Таким образом, закон сохранения механической энергии для данной системы имеет вид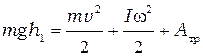 , (2.1)
, (2.1)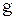 – ускорение свободного падения,
– ускорение свободного падения, 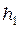 – высота, на которую поднят груз,
– высота, на которую поднят груз, 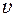 – скорость груза в нижней точке падения,
– скорость груза в нижней точке падения, 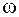 – угловая скорость маховика в тот же момент времени,
– угловая скорость маховика в тот же момент времени, 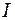 – момент инерции махового колеса,
– момент инерции махового колеса,  – работа по преодолению сил трения в подшипнике при движении груза вниз.
– работа по преодолению сил трения в подшипнике при движении груза вниз.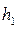 ,
, 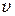 ,
,  Работа сил трения в подшипнике может быть найдена по формуле
Работа сил трения в подшипнике может быть найдена по формуле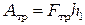 , (2.2)
, (2.2)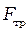 – сила трения в подшипнике, которую можно найти, исходя из следующих соображений. Если колесо не остановить, то оно, вращаясь по инерции, поднимет груз на меньшую высоту
– сила трения в подшипнике, которую можно найти, исходя из следующих соображений. Если колесо не остановить, то оно, вращаясь по инерции, поднимет груз на меньшую высоту 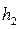 . Работа силы трения на всем пути
. Работа силы трения на всем пути 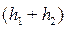 равна разности потенциальныхэнергий груза в конечном и начальном положениях, т. е.
равна разности потенциальныхэнергий груза в конечном и начальном положениях, т. е. ,
,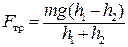 . (2.3)
. (2.3)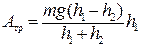 . (2.4)
. (2.4)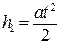 и
и 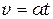 .
.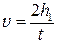 . (2.5)
. (2.5)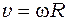 . В момент, когда груз находится в нижней точке траектории, угловая скорость махового колеса равна
. В момент, когда груз находится в нижней точке траектории, угловая скорость махового колеса равна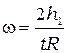 , (2.6)
, (2.6)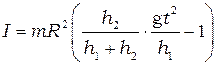 . (2.7)
. (2.7)


