Описание установки и метода измерений. Физическим маятником называется любое твёрдое тело, закрепленное на оси, не проходящей через его центр масс (рис
Физическим маятником называется любое твёрдое тело, закрепленное на оси, не проходящей через его центр масс (рис. 4.1). При отклонении маятника от положения равновесия на некоторый угол a сила тяжести
где
где Формула (4.2.) позволяет легко найти момент инерции маятника, если известно
В данной работе физический маятник (рис. 4.2) представляет собой однородный стержень 1, на котором крепятся опорные призмы 2 и 3 равной массы и два одинаковых груза 4 и 5. С помощью опорных призм маятник устанавливается на горизонтально закреплённую планку 6. Согласно формуле (4.2), момент инерции маятника относительно одной из осей (например, проходящей через опорную призму 2) равен
Но так как положение центра масс маятника
где L – расстояние между опорными призмами. Уравнения (4.3) и (4.4) содержат три неизвестные величины. Для нахождения моментов инерции необходимы дополнительные уравнения.
где Решив систему из четырёх уравнений (4.3), (4.4), (4.5) и (4.6), получают формулу для расчета положения центра масс маятника
Вычислив
|

 , приложенная в его центре масс С, создает момент силы, возвращающий маятник в положение равновесия. Момент силы тяжести относительно оси
, приложенная в его центре масс С, создает момент силы, возвращающий маятник в положение равновесия. Момент силы тяжести относительно оси  , согласно (Т.8), равен
, согласно (Т.8), равен , (4.1)
, (4.1)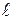 – расстояние от оси вращения маятника О до его центра масс С,
– расстояние от оси вращения маятника О до его центра масс С,  – плечо силы тяжести, знак " –" указывает на то, что момент силы возвращает тело в положение равновесия.
– плечо силы тяжести, знак " –" указывает на то, что момент силы возвращает тело в положение равновесия. Под действием возвращающего момента маятник совершает гармонические колебания с периодом, равным (вывод периода колебаний физического маятника дан в приложении к данной работе):
Под действием возвращающего момента маятник совершает гармонические колебания с периодом, равным (вывод периода колебаний физического маятника дан в приложении к данной работе):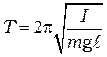 , (4.2)
, (4.2) – период колебаний маятника,
– период колебаний маятника, 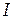 – момент инерции маятника относительно оси вращения О,
– момент инерции маятника относительно оси вращения О, 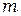 – его масса,
– его масса, 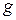 – ускорение свободного падения.
– ускорение свободного падения.
 .
. . (4.3)
. (4.3)
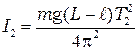 , (4.4)
, (4.4)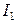 и
и  :
: , (4.5)
, (4.5)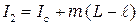 , (4.6)
, (4.6) – момент инерции стержня относительно оси, проходящей через центр масс стержня параллельно осям вращения.
– момент инерции стержня относительно оси, проходящей через центр масс стержня параллельно осям вращения.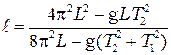 . (4.7)
. (4.7)


