Порядок выполнения работы. 1. Закрепить грузы на стержне так, как укажет преподаватель
1. Закрепить грузы на стержне так, как укажет преподаватель. 2. Измерить расстояние между опорными призмами L. 3. Установить маятник одной из опорных призм на площадку 6. Привести его в колебательное движение, отклонив на угол не более 15–20°, и измерить время 20–30 полных колебаний. Измерения проделать не менее 3-х раз. Найти среднее время колебаний á t 1ñ. 4. Перевернуть маятник и опять не менее 3-х раз найти время 20–30 полных колебаний, а затем – среднее время á t 2ñ. 5. Рассчитать периоды колебаний маятника Т 1 и Т 2 по средним значениям времени. 6. Рассчитать положение центра масс маятника 7. Рассчитать моменты инерциимаятника 8. Результаты измерений и вычислений занести в таблицу
Контрольные вопросы 1. Чему равен момент инерции точки, твердого тела? От чего зависит момент инерции? Каков его физический смысл? 2. Что такое центр масс тела (системы тел), каковы его свойства? 3. Сформулируйте теорему Штейнера. Поясните смысл величин в (4.5) и (4.6). 4. Чему равен момент силы относительно точки и относительно оси? 5. Момент какой силы заставляет физический маятник совершать колебательное движение? Чему равен его модуль и как он направлен? 6. Разложите силу тяжести на составляющие. Чему равен момент каждой из составляющих сил? 7. Выведите формулу периода колебаний физического маятника исходя из основного закона динамики вращательного движения (см. приложение). 8. Выведите формулы для расчета моментов инерции Приложение (вывод периода колебаний физического маятника) Основной закон динамики вращательного движения (Т.13) для физического маятника с учетом (4.1) имеет вид
где Так как синусы и тангенсы малых углов примерно равны самим углам в радианах, то sina @ a, и (4.8) принимает вид
где Решив дифференциальное уравнение (4.9), находят, что
Итак, угол отклонения маятника от положения равновесия изменяется по закону косинуса (синуса), т. е. маятник совершает гармоническое колебательное движение. Анализ уравнения (4.11) показывает, что amax и j0 – амплитуда и начальная фаза колебаний, а w0 – циклическая частота, связанная с периодом колебаний соотношением
Воспользовавшись обозначением (4.10), из (4.12) получают (4.2). Литература 1. Савельев И. В. Курс физики. Т. 1. – М.: Наука, 1989. – С. 94–116. 2. Трофимова Т. И. Курс физики. – М.: Высш. шк., 2001. – С. 34–46. Работа 1.5
|

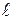 с помощью (4.7).
с помощью (4.7).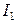 и
и  по формулам (4.3) и (4.4).
по формулам (4.3) и (4.4). , (4.8)
, (4.8) – угловое ускорение маятника.
– угловое ускорение маятника. , или
, или 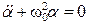 , (4.9)
, (4.9)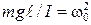 . (4.10)
. (4.10) . (4.11)
. (4.11) . (4.12)
. (4.12)


