Описание установки и метода измерений. На рис. 6.1 показано сечение сферического зеркала MLN плоскостью чертежа
На рис. 6.1 показано сечение сферического зеркала MLN плоскостью чертежа. L – наинизшая точка зеркала. Если шарик поместить в произвольную точку С, а затем отпустить, он будет совершать колебательное движение.
Рис. 6.1 Для нахождения радиуса кривизны зеркала R используют закон сохранения механической энергии. В точке С механическая энергия шарика равна его потенциальной энергии Если пренебречь трением между шариком и поверхностью зеркала, то закон сохранения механической энергии для шарика будет иметь вид
где Учитывая, что момент инерции шарика
Высоту h, на которую поднимается центр масс шарика при его отклонении от положения равновесия, можно выразить через радиус кривизны поверхности, по которой движется центр масс шарика
Если в последнем выражении раскрыть скобки и пренебречь величиной второго порядка малости (каковой является
Для нахождения скорости шарика необходимо знать уравнение его движения. Шарик совершает затухающие колебания, но при расчете радиуса кривизны не будет большой ошибкой считать, что он совершает незатухающие колебания, так как при малых коэффициентах затухания периоды затухающих и незатухающих колебаний различаются незначи-тельно. Итак, будем считать, что шарик совершает гармоническое колеба-тельное движение, описываемое уравнением
где x – смещение шарика от положения равновесия в момент времени t,
Взяв первую производную от смещения (6.4) по времени, получим скорость шарика как функцию времени
Из (6.6) следует, что максимальное значение скорость имеет при
Подставив (6.7) и (6.3) в (6.2), получим формулу для расчёта радиуса кривизны поверхности, по которой движется центр масс шарика
Как видно из (6.8), для расчета R¢ необходимо знать только период колебаний шарика, который легко найти, измерив время t, за которое шарик совершает n колебаний: Из рис. 6.1 видно, что радиус кривизны поверхности зеркала R равен
|


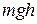 , так как шарик неподвижен, а в точке L механическая энергия шарика равна его кинетической энергии, которая слагается из кинетической энергии поступательного движения
, так как шарик неподвижен, а в точке L механическая энергия шарика равна его кинетической энергии, которая слагается из кинетической энергии поступательного движения 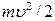 и кинетической энергии вращательного движения
и кинетической энергии вращательного движения  .
. , (6.1)
, (6.1)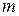 – масса шарика, h – высота точки С по отношению к точке L,
– масса шарика, h – высота точки С по отношению к точке L, 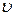 – скорость поступательного движения шарика в точке L, ω – угловая скорость вращательного движения шарика в той же точке, I – момент инерции шарика относительно оси, проходящей через его диаметр.
– скорость поступательного движения шарика в точке L, ω – угловая скорость вращательного движения шарика в той же точке, I – момент инерции шарика относительно оси, проходящей через его диаметр.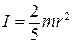 , и, согласно (Т.5),
, и, согласно (Т.5), 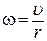 (где r – радиус шарика), уравнение (6.1) можно преобразовать
(где r – радиус шарика), уравнение (6.1) можно преобразовать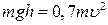 . (6.2)
. (6.2) . Рассмотрим треугольник COD, в котором ОС = R¢, ОD = R¢ – h, DC = A (отрезок DC можно считать равным амплитуде колебаний шарика А, так как при сравнительно малых отклонениях от положения равновесия хорда и стягиваемая ею дуга практически совпадают). Поскольку треугольник СОD прямоугольный, то для него можно записать теорему Пифагора
. Рассмотрим треугольник COD, в котором ОС = R¢, ОD = R¢ – h, DC = A (отрезок DC можно считать равным амплитуде колебаний шарика А, так как при сравнительно малых отклонениях от положения равновесия хорда и стягиваемая ею дуга практически совпадают). Поскольку треугольник СОD прямоугольный, то для него можно записать теорему Пифагора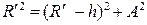 .
. ), то получим, что
), то получим, что . (6.3)
. (6.3) , (6.4)
, (6.4)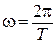 . (6.5)
. (6.5)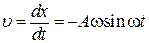 . (6.6)
. (6.6) . (6.7)
. (6.7)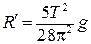 . (6.8)
. (6.8)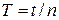 .
.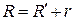 . (6.9)
. (6.9)


