Подвеска
Вследствие возмущающего воздействия неровностей дороги и наличия в подвеске упругого элемента движение автомобиля всегда сопровождается его колебаниями. При движении по часто чередующимися неровностям возникают вынужденные колебания. Их частота находится в сложной зависимости от профиля дороги, скорости движения и конструктивных параметров автомобиля, т.е. от условий, сочетания которых носят случайный характер. Эти колебания здесь не рассматриваются. Установлено, что частота собственных колебаний подрессоренной массы автомобиля зависит только от величины статического хода hc. Поэтому частоту используют в качестве одной из основных характеристик подвески. При построении основной эквивалентной колебательной системы для определения собственных частот подрессоренных масс, характеризующих плавность хода автомобиля, достаточно отразить в ней только факторы, вызывающие линейные перемещения z и угловые перемещения (подрессоренной массы, и рассматривать ее без учета влияния неподрессоренных масс, демпфирования и возмущающих факторов (рис. 1.5). При рассмотрении принимаем, что автомобиль симметричен относительно продольной плоскости, поэтому рассмотрим плоскую модель.
Подрессоренной частью автомобиля являются все его элементы, масса которых передается упругими элементами подвески (кузов, рама). Те элементы, масса которых не передается через упругие элементы подвески, называют неподрессоренными элементами автомобиля (колеса в сборе, детали направляющих устройств, включая неподрессоренные мосты, часть массы упругих элементов и Кинетическая и потенциальная энергии рассматриваемой системы
K = 0, 5mnz2 + 0, 5да„ pp2, П = 0, 5cn (z + ap)2 + 0, 5c3)(z - bp)1. Дифференцируя систему уравнений (1.27) по обобщенным координатам и подставляя значения производных в уравнение Лагранжа, получим систему дифференциальных уравнений вертикальных и продольно-угловых колебаний mnz + z(cn + C3 ) + p(cna - cb) = 0 mn p(+ p(Cna2 + c3b2) + z (cna - c3b) = 0, (128) где c = C C /(c + C), n pn шп \ pn ш n/' c = C C /(c + C), 3 p3 Ш3 \ p3 ШЗ mn - подрессоренная масса, cpn, cp3 - приведенная жесткость упругих элементов, соответственно, передней и задней подвесок, c0n, c03 - жесткость шины, соответственно, передних и задних колес, p - радиус инерции подрессоренной массы автомобиля. Система дифференциальных уравнений (1.28) показывает, что в общем случае координаты z и p связаны между собой. Если сместить кузов параллельно самому себе в направлении оси z, а затем внезапно отпустить, то отмечаются не только вертикальные перемещения z, но и угловые с углом поворота p. Координаты z и p независимы только при cna — c3b = 0. В этом случае приложенная сила к центру массы вызывает только вертикальное смещение без поворота. Тогда уравнения (1.28) примут вид mnz + z(Cn + C3 ) = ^ mn ppp + p(cna2 + c3b2) = 0, (129) Соответствующие этим уравнениям собственные частоты c + с c a + с b ^ =\ ^^, ®p=J n p23. (1 30) V mn V mnP Из условия равенства частот вертикальных и угловых колебаний, принимая, что колебания передних и задних подрессоренных частей независимы и справедливо условие: cn = с3 (b / a), получим, что вертикальные и угловые колебания будут равны при p2 = ab. Собственные частоты передней и задней частей подрессоренных масс можно выразить через соответствующие массы и жесткости m v m n v nn (1.31) cb /( a + c, ) = cn
mn mn3
Здесь mm = mnb /(a + b) и mns = mna /(a + b). Таким образом, при принятых допущениях эквивалентную систему автомобиля можно представить как состоящую из двух подрессоренных передней и задней масс mnn и mm и опирающихся на, сответственно, пружины с приведенными жесткостями cn и c3. При значениях р2 /ab = 0, 8...1, 2 колебания подрессоренных масс над передней и задней осями являются практически несвязанными и, следовательно, для нахождения частот свободных колебаний можно пользоваться формулами (1.31). Частота колебаний в минуту связана с угловой частотой соотношением 30оп 30 [c~ Пп =------ " =---- J^. (1.32) п п у mn Если выразить через статический прогиб fcm, то
m g 300 Y^- —f= • (1.33)
Jcmmnn У/ J cm В среднем величину fd можно принять следующей: легковые автомобили........................ 0, 5 f автобусы............................................ 0, 75 f грузовые автомобили....................... 1, 0 f
Расчет упругих элементов подвески проводят исходя из нагрузки Rz3 на упругий элемент и по его прогибу f с учетом кинематики подвески и в зависимости от вертикальной реакции Rz на колесо и установленного статического прогиба подвески f (1.33). Для зависимой подвески с неразрезным мостом (рис. 1.7) определяют по вертикальной реакции
Rz на колесо за вычетом веса неподрессоренных частей: Rzs = Rz - у, (1.34) где ga - вес моста с колесами. Прогиб fy3 = f (1.35) Для независимой подвески с одним рычагом (рис. 1.8):
Rzs = (Rz - gk) -, (1.36) a где gk - вес колеса и часть веса рукава разрезного моста или направляющего устройства подвески.
Для независимой подвески на двух рычагах (рис. 1.9):
Для стержневых независимых подвесок момент, закручивающий стержень, определяется в зависимости от кинематики подвески. Для неуправляемого колеса (рис.1.10) M = (Rz -gk)L. (139) Угол закрутки стержня (в радианах) 0=f.
L
Для управляемого колеса с независимой подвеской (рис. 1.11) M = (Rz - gk)р, 0 = f.
При расчете направляющих устройств подвески исходят из трех случаев нагружения, рассмотренных при расчете ведущего и управляемого мостов. В первом расчетном случае нагружения действуют вертикальная Rz и горизонтальная Rx силы, боковое усилие Ry отсутствует (рис. 1.12). Сила Rz на плече (L - р1) создает момент, уравновешиваемый моментом на вертикальной стойке.
Возникающие при этом силы
P'= P'= Rz(L -р)/р2. (1.43) Тормозная сила создает на MT = Rxr p' = Rx (ba / Р2). Тормозная сила Rx относительно шарниров создает также момент, стремящийся повернуть колеса относительно шкворня. Этот момент уравновешивается моментом от силы P, действующим на поперечную рулевую тягу. Сила P = Rx (L - р1) /1 обусловливает в шарнирах стойки возникновение сил Pp и PP: PP = Rxi [(L -p)/ l](b /p2) PP = Rx! [(L-p)/l](a0 /P2). (1.46) Таким образом, верхний рычаг работает на сжатие или продольный изгиб от усилий (р - P') и (PM -P'), а нижний - на изгиб от усилий Rz, Pnp и (PM + Px"), а также на растяжение от усилия (PP+PP). При втором случае нагружения учитывают вертикальные силы, действующие на колеса Rzn и Ryn, а также боковые силы Ryn и R„n (рис. 1.13). При этом Rx = 0. Сила Rzn создает момент и нагружает рычаги усилиями
PL = PPn= Rzn (L -a)/P2. (1.47) Боковая сила создает усилия на рычагах р; = Ryn(bo / Р2) pyn = Ryn(ao / P2). (1^48) Момент, обусловленный боковой силой, создает в рычагах силы PL = PL = Ryn (r / P2). (1.49)
|

 Рис.1.5. Приведенная модель автомобиля
Рис.1.5. Приведенная модель автомобиля
 Рис.1.6. Упругая характеристика подвески
Рис.1.6. Упругая характеристика подвески
 Рис.1.7
Рис.1.7
 Рис.1.8
Рис.1.8
 Рис.1.9
Рис.1.9
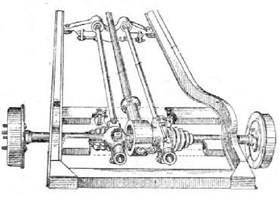
 Рис.1.11
Рис.1.11
 Рис.1.12. Расчетная схема подвески Под действием тормозной силы на шарнирах возникают силы
Рис.1.12. Расчетная схема подвески Под действием тормозной силы на шарнирах возникают силы
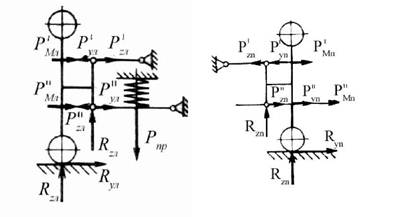 Рис.1.13. Расчетная схема подвески
Рис.1.13. Расчетная схема подвески




