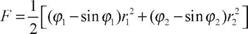Расчет элементов рулевого управления

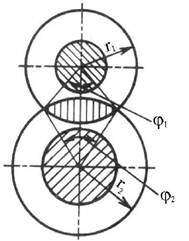
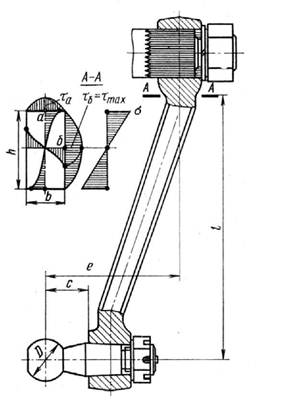
Нагрузки в элементах рулевого управления и рулевого привода определяются на основании следующих двух расчетных случаев:

- по заданному расчетному усилию на рулевом колесе;

- по максимальному сопротивлению повороту управляемых колес на месте.

При движении автомобиля по дорогам с неровной поверхностью или при торможении с различными коэффициентами сцепления под управляемыми колесами ряд деталей рулевого управления воспринимает динамические нагрузки, которые лимитируют прочность и надежность рулевого управления. Динамическое воздействие учитывается введением коэффициента динамичности к_д = 1, 5...3, 0.

Расчетное усилие на рулевом колесе для легковых автомобилей P_PK = 700 H. Для определения усилия на рулевом колесе по максимальному сопротивлению повороту управляемых колес на месте 166 Рулевое управление
необходимо рассчитать момент сопротивления повороту по следующей эмпирической формуле

M_c = (2р_о /3)V О^ъ_к/ р_ш,

где р_о - коэффициент сцепления при повороте колеса на месте ((р_о = 0, 9...1, 0), G_k - нагрузка на управляемое колесо, р_ш - давление воздуха в шине.

Усилие на рулевом колесе для поворота на месте

Р_ш = Mc /(u_aR_PKnPp_y),

где u_a - угловое передаточное число.

Если вычисленное значение усилия на рулевом колесе превосходит указанное выше условное расчетное усилие, то на автомобиле требуется установка рулевого усилителя. Рулевой вал. В большинстве конструкций его выполняют полым. Рулевой вал нагружается моментом

^МРК = ^PPK^RPK.

Напряжение кручения полого вала

т = M_PKD/[0, 2(D⁴ -d⁴)]. (8.4)

Допускаемое напряжение [т] = 100 МПа.

Проверяется также угол закрутки рулевогого вала, который допускается в пределах 5...8° на один метр длины вала.

Рулевой механизм. Для механизма, включающего глобоидный червяк и ролик, определяется контактное напряжение в зацеплении

о= Px /(Fn), (8.5)

P_x - осевое усилие, воспринимаемое червяком; F - площадь контакта одного гребня ролика с червяком (сумма площадей двух сегментов, рис. 8.4), и-число гребней ролика.

Осевая сила

Px = Мрк /(r_wotgP),

где r_wo - начальный радиус червяка в горловом сечении, Рис. 8.4 в - угол подъема винтовой линии в том же сечении.

 

Материал червяка-цианируемая сталь ЗОХ, 35Х, 40Х, ЗОХН; материал ролика- цементуемая сталь 12ХНЗА, 15ХН.

Допускаемое напряжение [а] = 7...8МПа.

Для винтореечного механизма в звене " винт-шариковая гайка" определяют условную радиальную нагрузку P₀ на один шарик

^Рш = ^5Px ^{/(mz COs}-$кон ⁾,

где m - число рабочих витков, z - число шариков на одном витке, 8_кон - угол контакта шариков с канавками (д_кон = 45^o).

Контактное напряжение, определяющее прочность шарика

(8.6)

где Е - модуль упругости, d_m - диаметр шарика, d_k - диаметр канавки, к_кр - коэффициент, зависящий от

кривизны контактирующих поверхностей (к_кр = 0, 6...0, 8).

Допускаемое напряжение [а_(Ж] = 2500..3500 МПа в зависимости от диаметра шарика. По ГОСТ 3722-81 может быть определена разрушающая нагрузка, действующая на один шарик.

Площадь контакта одного гребня ролика с червяком (рис.8.4)

Следует учитывать, что наибольшие нагрузки в винтовой паре имеют место при неработающем усилителе.

Зубья сектора и рейки рассчитывают на изгиб и контактное напряжение по ГОСТ 21354-87, при этом конусностью зубьев сектора пренебрегают. Окружное усилие на зубьях сектора

^Рсек = ^МРкЬмЪм ^{/ r}ceK + Р^Щ ^/4,

где r_ceK - радиус начальной окружности сектора, р_ж - максимальное давление жидкости в усилителе, Е_гц - диаметр гидроцилиндра усилителя.

Второе слагаемое применяется в том случае, если усилитель нагружает рейку и сектор, т. е. когда рулевой механизм объединен с гидроцилиндром.

Материал сектора - сталь 18ХГТ, ЗОХ, 40Х, 20ХНЗА, [а_и] = 300...400 МПа, [о_сж] = 1500 МШ.

Вал рулевой сошки. Напряжение кручения вала сошки при наличии усилителя

 

/(0, 2d3),

(8.7)

т =

^МРК*Р_МПРМ + Р_ж^п 4

 

где d - диаметр вала сошки, р_ж - максимальное давление жидкости в усилителе, D_ry - диаметр гидроцилиндра усилителя.

Материал вала сошки - сталь 30, 18ХГТ, 20ХНЗА. [т] = 300...350 МПа. Рулевая сошка (рис. 8.5).

Расчет ведут на сложное сопротивление. Шлицы (рифты) рассчитывают на срез. Усилие на шаровом пальце сошки, вызывающее изгиб и кручение (при наличии встроенного усилителя),

^Poo0 = ^МРК*РМПРМ ^{/ 1} + РПщ ^{/ 41}. Напряжение изгиба в опасном сечении А-А

= POJ/W. (8.8)

Напряжение кручения

т= P«J/Wk, (8.9)

где W_u и W_k - соответственно осевой и полярный моменты сопротивления опасного сечения.

(8.10)

Эквивалентное напряжение рассчитывается по третьей теории прочности. Материал сошки: сталь 30, Рис. 8.5. Расчетная схема рулевой сошки 18ХГТ, [< У_экв] = 300...400 МПа.

Шаровой палец сошки. Напряжение изгиба

^u = PoJ / Wu.

(8.11)

Материал: сталь 40X, 20XH3A. Допускаемое напряжение [c_u] = 300...400МПа. Напряжение смятия (давление, которое определяет износостойкость шарового пальца с диаметром шара d„,)

q = 4 P oo0 /(nd0), [q] = 25...35 МПа. Рулевое управление

Напряжение среза при площади сечения шарового пальца у основания

о_ср = Роо0 /F_m, [о_ср] = 25...35 МПа. (8.12)

Продольная тяга (рис.8.6). Сила Р_со0 вызывает напряжение сжатия-растяжения и продольного изгиба тяги.

Напряжение сжатия

о_{< ж} = Рсо0 /F, (8.13)

где F - площадь поперечного сечения тяги.

Критическое напряжение при продольном изгибе

Окр =П EJ /(L_TF), (8.14)

где L_T - длина прдольной тяги, J = n(D⁴ -d⁴)/64 - момент инерции поперечного сечения.

Запас устойчивости тяги

8=°_кр /о_сж =ж²EJ /(P_comLT).

Материал: сталь 20, сталь 35.

Поворотный рычаг. Поворотный рычаг нагружается изгибающей силой Р_со0 и скручивающим моментом Р_сош1.

Напряжение изгиба

Ои = Р_тш*/Wu. (8.15)

Напряжение кручения

^ = P_mJ/Wk. (8.16)

Материал: сталь 30, сталь 40, 40ХГНМ. [о_же] = 300...400 МПа.

lolu

Рис.8.6

Боковые рычаги трапеции. Боковые рычаги трапеции испытывают напряжение изгиба и кручения под действием силы Р_пт = Р_сош$ /1.

Напряжение изгиба

 

(8.17)

и

и

Ои = Рпт1 / Wu

пт

 

Напряжение кручения

 

Т = Рпт1 / W_k.

Материал: сталь 30, сталь 40, 40ХНМ. [о_экв] = 300...400МПа.

Поперечная тяга трапеции. Поперечная тяга трапеции нагружена силой Р_пт и рассчитывается по той же методике, что и продольная тяга. Для изготовления поперечной тяги используется тот же материал, что и для продольной.