Тел на ее поверхности
Пульсация Земля и изменение веса тел на ее поверхности
Выше показано, что все тела, включая звезды, планеты, спутники элементарные частицы и т.д., обладают самодвижением – пульсацией и что эта самопульсация обусловливает движение всех тел в пространстве. Тем не менее, современные наблюдения движения планет как бы не подтверждают этих утверждений, хотя астрономы теоретически уже начали описывать гармонику вибраций планет [106] (вибраций, а не пульсаций, что не одно и тоже) с периодом от нескольких минут до суток и более, с амплитудой от 1 до 3 см., что, конечно же, для параметров Земли весьма и весьма недостаточно и современными приборами вроде бы обнаружено быть не может. Но так ли это? Начнем с простого вопроса: Что такое вес? Ответ на этот вопрос можно отыскать в любом физическом справочнике. Например, в [35] находим: «Весом тела называется сила Р, с которой оно действует вследствие тяготения к Земле на опору или подвес, удерживающие его от свободного падения. При этом предполагается (т.е. постулируется – А.Ч.), что тело и опора (или подвес) неподвижны относительно системы отсчета, в которой определяется вес тела». В таком определении неявно постулируется так же центральное притяжение тела и невозможность фиксации веса без прямого воздействия тела на опору или подвес. Как, например, чашечка весов не зафиксирует наличие веса, если на нее не положено некое тело. Добавлю – что в определении сама инерциальная система отсчета (т.е. система, не взаимодействующая с окружающем пространством) предполагается (опять же постулируется) неподвижной и неизменной. Поэтому вес тела Р в системе отсчета, связанной с Землей равен силе тяжести тела F и не может изменяться во времени. А это означает, что в современной механике инерциальная система отсчета – Земля независима по определению (т.е. по тому же постулату) от воздействия пространственной плотности области в котором она находится при орбитальном движении, (т.е. постулируется, что в каждой области планета тождественна самой себе), и поэтому не изменяет своих параметрови все тела на ее поверхности, как и она сама, не взаимодействуют ни с планетой, ни с окружающими космическими телами и потому тоже неизменны. Здесь − логическое противоречие. По классической механике Земля на орбите движется по инерции, т.е. без всякого взаимодействия с окружающим пространством, и потому может считаться инерциальной системой отсчета. Но гравитационное поле Солнца притягивает планету (т.е. воздействует на нее), изменяя направление движения. А это воздействие меняет характер движения, придавая ему другое качество и превращая его из движения без взаимодействия в движение взаимодействия, т.е. в неинерциальное движение. Поскольку Земля взаимодействует с гравиполем Солнца, то ее движение не может быть инерциальным, и вследствие этого она не может выполнять функции инерциальной системы отсчета. И ничем не обоснованы ссылки на то, что размеры Земли несопоставимы с величиной ее орбиты, и поэтому можно на небольшом отрезке траектории считать (постулировать) планету точкой, т.е. инерциальной системой отсчета. Выше показано, что размер зоны её влияния (макромолекулы) всего на два порядка меньше расстояния до Солнца, а это уже величины, которые невозможно свести к точке. К тому же существует физический механизм, обусловливающий гравитационное взаимодействие светила и планеты и отображающий характер движения Земли. (Если Земля точка, то о взаимодействии и речи быть не может.) И этот механизм скрывается как за пресловутой абстракцией – «точка», так и за постулируемой неизменностью параметров входящих в закон всемирного тяготения. Придание Земле функции системы отсчета, нарушило структуру и принципы отображения тел в физике. В частности «отключился» один из основных принципов [2] – принцип взаимосвязи свойств, который можно сформулировать так: 1. Каждое тело – система, имеющая бесчисленное множество качественно взаимосвязанных как внутренних, так и внешних равнозначных свойств. Из него следует, что современное понятие – «Земля», как инерциальная система отсчета, не включает в свою структуру взаимосвязи с окружающим пространством, что автоматически разрывает внешние связи планеты, (превращая ее в замкнутую систему) и обусловливает неизменность ее параметров, как и параметров тел на ее поверхности, в любой области орбиты. Это конечно возможно, но только в идеальном случае — если планета не вращается вокруг своей оси и движется в телесном пространстве по абсолютно круговой траектории (т.е. является абстракцией). Земля, однако, имеет качественно иную, эллиптическую траекторию и вращается вокруг своей оси. В своем движении по орбите она проходит области с различной напряженностью гравитационных полей. И нельзя исключить, что напряженность внешнего гравитационного поля, которое меняется по мере ее движения по орбите, воздействует на Землю, изменяя количественно величину ее параметров: собственную напряженность гравитационного поля, массу, радиус, гравитационную «постоянную» и др., пропорционально скорости прохождения её через внешнее поле. Вызываемое изменением напряженности внешнего гравитационного поля численные величины параметров планеты не фиксируется на сегодня физическими приборами только потому, что синхронно и пропорционально ему происходит изменение параметров всех тел, находящихся на поверхности планеты, включая человека и приборы, которыми он пользуется. И поэтому непосредственное наблюдение пульсации на поверхности планеты достаточно затруднено. Естественно так же, что изменение напряженности гравиполя Земли, как и других параметров, должно оказывать влияние на все свойства тел, находящихся на ее поверхности, включая их вес и объем. Не исключено, что именно вес может фиксироваться весами, и опосредовано отображается на результатах эмпирического определения численной величине гравитационной «постоянной» G. С приложением к Земле понятия инерциальной системы отсчета в физике перестал «работать» и принцип инвариантности, который можно сформулировать следующим образом: 2. Количественные изменения величины любого внешнего или внутреннего свойства системы (тела) отображаются пропорциональным изменением численных величии (модулей) всех остальных свойств и его положения в пространстве (или деформацией объема, если тело не может изменить своего положения). Из этого принципа следует, что все свойства (параметры) тел могут быть формализованы в виде уравнений-инвариантов с различным количеством членов. И изменение численной величины любого из параметров этого инварианта должно сопровождаться в уравнениях пропорциональным изменением всех остальных его членов. Ниже будет рассмотрено применение этого принципа к орбитальному движению планеты. Однако современное представление о Земле, как об инерциальной системе отсчета, не взаимодействующей с внешней средой, накладывает табу на эти изменения и тем самым вычленяет Землю из Солнечной системы, превращая ее в мертвый символ той математической конструкции, в которой она задействована. Если же, исходя из самопульсации планеты (и других планет), предположить, что под влиянием изменения гравиполя Солнца все параметра Земли (включая радиус и массу) меняются, то следствием пульсации будет изменение расстояния между центрами масс тел во времени, и, следовательно, пропорциональное изменение веса тел на поверхности Земли. И это изменение внешнего гравиполя в афелии и перигелии может достигать значительных величин и должно наблюдаться в экспериментах, надо только найти методику таких наблюдений. Однако нахождению методики пульсации мешают постулаты и законы классической механики, и в первую очередь закон всемирного тяготения. Отмечу, что, похоже, ни в одном справочнике, ни в одном учебнике при определении понятия «вес» не отмечается, к какой же физической категории относится это понятие. Известно, что сила F, как и другие свойства тел, есть неотъемлемое свойство любого тела (в том числе и элементарной частицы), которое не может быть изъято у тела не может исчезнуть иначе как с исчезновением тела (такое понимание свойств осознали еще не все учёные). Понятие же «вес» как свойство не воспринимается, поскольку, по представлению классической механики, возможно и такое состояние тела, при котором у него отсутствует вес, — состояние «невесомости». И в этом случае, по той же механике, сила притяжения тела к планете остается (как бы компенсируется скоростью вращения па орбите), а вес у тела исчезает. Следовательно, вес не является свойством и он не эквивалентен силе притяжения, хотя на поверхности Земли и «совпадает» с ней. Чем же он в таком случае является? Классическая механика не объясняет это различие, а просто констатирует численное равенство веса тела на поверхности и силы притяжения его планетой. Сила «притяжения» между двумя телами F или, что то же самое, вес Р определяется законом всемирного тяготения И. Ньютона. Следствием, предполагаемой еще со времен И. Ньютона, независимости (неявно постулируемой) параметров Земли от области пространства Солнечной системы, в котором она находится, стало постулирование, в уравнении тяготения параметров m, М, R, F, а позже и G постоянными величинами во времени с любой степенью точности. Если в первом приближении исходить из того, что Земля, как система отсчета, имеет форму шара, то закон всемирного тяготения, как показано выше, формулируется в виде: F = Р = GMm/R2, (4.1) где: F – сила, с которой тело давит на поверхность планеты, постулируется неизменной, Р – вес тела, неизменный по той же причине, G – гравитационная «постоянная», предполагается (постулируется), что этот коэффициент пропорциональности материальных точек единичной массы не может изменяться, так как единичные массы не меняются, М – масса Земли (всегда и везде постулируется постоянной), m – масса тела (тоже постулируется постоянной). Наконец R – расстояние между центрами масс тоже неизменно, поскольку, по предположению (по постулату), отсутствуют силы, способные деформировать планету и потому она не может пульсировать. (Не слишком ли много постулатов для одной формулы? И сколько же их тогда в современной физике?) Так как размеры практически любого тела на поверхности Земли несопоставимы с ее радиусом, то расстояние между центром масс тела и планеты равно радиусу планеты, а тело в уравнении (4.1) представляет собой точку с массой m, т.е. телом не является по определению. Поскольку все параметры, входящие в (4.1), по современным представлениям неизменны, то о возможности изменения веса тел и говорить не приходится, тем более что (4.1) оказывается единственным уравнением, используемым для определения веса тел, если не считать производного от него уравнения силы притяжения – mg: F = Р = mg, (4.2) где g = GМ∕ R2 – напряженность гравитационного поля (ускорение свободного падения). В процессе движения Земли по эллиптической орбите постоянно и зримо меняются два параметра – скорость и расстояние до светила. То, возрастая, то, убывая, они как бы демонстрируют годовой период пульсации планеты. Поэтому, в соответствии с принципом инвариантности, появляется возможность отслеживать изменение этих параметров и ожидать одновременного, и пропорциональ-ного количественного изменения всех других параметров Земли: массы, объема, напряженности гравитационного поля и т.д. А вместе с ними изменение численной величины всех свойств тел, находящихся на поверхности планеты. Из этих свойств проще всего наблюдать изменение веса и объёма у тел на поверхности Земли. Возможность же выявление изменение веса тел во времени, при простоте проведения эксперимента, является достаточно веским основанием для эмпирической проверки указанных предположений. Эти предположения подвигли к тому, что в 2005 году в НПО «Квант-Элемет» (НПО Квант-Элемет, отдел Н.С. Лидоренко) был начат, как уже упоминалось, эксперимент по длительному ежедневному (кроме выходных дней) наблюдению за изменением веса четырех твердых тел из не намагничивающихся материалов. Были взяты: дубовый брусок, брусок из полимера, брусок дюралевый и свинцовый цилиндр (параметры их на начало эксперимента см. в таблице 10 стр. 209.). Для наблюдения за изменение веса использовались лабораторные весы ВЛ-500. Целью эксперимента было: в течение годового промежутка времени определить экспериментально, на качественном уровне, изменяется ли вес указанных тел, тенденцию и примерный порядок этого изменения, если оно имеется. Естественно, что эксперименты по изучению колебания веса тел во времени следует проводить в термостате и в вакуумной камере. Но не исключалась и возможность получение заметных результатов на лабораторных весах, поскольку прикидка влияния внешних воздействий (температуры, давления, влажности и т.д.) на изменение веса тел во времени показала, что их совокупное воздействие может вызывать изменение веса только до пятого знака. К тому же используемые в эксперименте тела имеют различные размеры, плотность, влагонасыщаемость и т.д., и потому указанные факторы должны вызывать некоррелируемое изменение веса тел в процессе взвешивания за год. Известно, что изменение веса, при взвешивании одного тела, оказывается строго пропорциональным изменению массы Земли, что, с высокой точностью (10-8-10-9), демонстрируют гравиметры. Это подтвердило и длительное ежедневное (кроме выходных) взвешивание двух контрольных грузов-эталонов из одного материала. Вес их на протяжении трех лет оставался неизменным. Эксперимент проводился простым взвешиванием эталонных тел, и результаты оправдали ожидания. Оказалось, что вес всех тел изменяется во времени в различных пропорциях, а это свидетельствует о том, что получаемые численные изменения веса определяются свойствами тел. Количественные результаты измерения показаны в таблице 11 (стр.209): Экспериментальное определение веса тел в одном месте в разное время года показывает, что вес их во времени меняется в четвертом, а иногда и в третьем знаке (при весе тела в пределах 200-500 гр.). И это изменение не находит доказательного объяснения. Попытки связать изменение веса тел во времени с воздействием других планет Луны и Солнца оказались не эффективными.
Здесь же, заодно, отметим следующие факторы, сопровождавшие изменение веса: • на графике заметно, что вес всех тел на последний день проведения эксперимента оказался больше чем в первый день наблюдения; • колебания веса тел коррелировало между собой и происходило одновременно (и для дубового бруска) но количественная величина их была различной. Наблюдался ряд эффектов в изменениях веса тел; • не мгновенную реакцию тел на изменение внешнего гравиполя. Создается впечатление, что эта реакция, в какой-то мере связана с плотностью тел; • в весенне-летние месяцы деревянный брусок реагирует на изменение напряженности гравиполя слабее, чем в осенне-зимний период; • брусок из оргстекла как бы слегка отображает «поведение» бруска из дуба; • в зимний период отмечалось синхронное изменение веса всех тел при значительных температурных перепадах (выделяются 20-30о морозы января – февраля 2006 г.). Вывод: Земля пульсирует в гармонике нескольких периодов (в том числе с годовым периодом). Изменяющаяся в течение года вдоль орбиты напряженность гравиполя Солнечной системы деформирует параметры планеты, что отражается на весе тел, находящихся на ее поверхности. Повторюсь: на графике5 отчетливо просматривается корреляция изменения веса тел за годовой промежуток времени, хотя количественные величины изменений не совпадают. Диаграммы изменения веса неорганических тел достаточно тесно коррелируют между собой, отображая не случайный характер этого изменения во времени. А, следовательно, должны существовать некоторые внешние или внутренние факторы, обусловливающие данные изменения. Поскольку наблюдалась корреляция времени года с изменением веса, было высказано предположение, что оно связано с орбитальным движением планеты. И это предположение подтвердилось. В астрономии используется система таблиц – эфемерид предсказывающая на перспективу по дням скорости движения планет вокруг Солнца и их расстояния до него. Для определения ежедневной скорости планеты на орбите и расстояния от Земли до Солнца использовались таблицы эфемерид лаборатории реактивного движения (Калифорния, США) за 2005-2006 гг. Таблицы определяют основные прогнозируемые параметры орбитального движения планет на несколько лет. Отмечу, — эфемериды рассчитываются исходя из предположений о том, что космическое пространство невещественно, изотропно от точки к точке, не имеет плотности и не оказывает никакого влияния на перемещающиеся в нём тела (планеты). Изотропность, в свою очередь, предполагает единую для всего пространства метричность. Само тело — планета, как система отсчета, в процессе инерциального движения по орбите не меняет своих размеров (не пульсирует), ее масса и радиус тоже не изменяются, а радиус орбиты изменяется достаточно монотонно. Воспользуемся эфемеридами и попытаемся выяснить, используя инвариантные уравнения из [2], коррелируют ли изменяющиеся параметры планеты, в ее орбитальном движении, с изменением веса тел на ее поверхности. Способы получения инвариантов кратко изложены выше и в работах [15, 43]. Ежедневная скорость и величина радиуса орбиты планеты приведены в приложении 2 столбцы R 1и v. Усреднив эти величины понедельно, выберем один из исследуемых предметов, например, свинец, и, приведя модуль средненедельной орбитальной скорости планеты к сопоставимой с модулем аналогичного изменения веса свинцового цилиндра, сравним на графике диаграммы их изменения за год (график 6). На графике 6 видно, что изменение модулей скорости и веса происходит разнонаправлено, но, тем не менее, коррелирует друг с другом, только диаграмма веса несколько сдвинута влево относительно диаграммы скорости. Отмечу, что диаграмма скорости на графике 6 отображает волнообразное ежемесячное
График 6. График 7. изменение скорости движения планеты, которое в принципе не допускает классическая механика, поскольку оно ставит под сомнение движение планеты по инерции. Проведем аналогичное построение графика понедельного изменения веса свинца на поверхности планеты и радиуса орбиты (график 7.). Диаграммы изменения веса свинца и радиуса орбиты однонаправлены и корреляция их изменения, так же, как и сдвиг влево диаграммы веса, проявляется более четко. Поскольку изменение скорости орбитального движения планеты и радиуса орбиты жестко связаны между собой инвариантом: Rv2 – const, (4.3) то можно предположить, что скорость, на графике 6отображает наблюдаемую (фактическую) величину, а расстояние от планеты до светила (граф. 7.) – величину расчётную, полученную независимо от скорости движения планеты. А если допущен расчет радиуса орбиты без учета скорости движения планеты, то следует ожидать, что вследствие этой ошибки в афелии и перигелии не будут совпадать дни экстремальных значений скорости и радиуса, хотя средний радиус орбиты может остаться неизменным, а возрастет большая полуось и коэффициент эллиптичности. Совместим графики 2 и 3 на графике 8 и получим качественную картину в диаграммах взаимосвязи движения планеты и изменения веса тел на ее поверхности.
Констатируем: Изменения веса свинца во времени (как и оргстекла и дюралевого бруска) коррелирует с пропорциональным изменением орбитальной скорости и радиуса планеты. С первого октября 2008 года ежедневное взвешивание четырех различных тел стали проводить в Перми (С.Гусаров)и в Челябинске (А. Королёв). Одно из них – дерево три другие: оргстекло, дюраль, свинец. Из них наименьшего доверия заслуживают результаты взвешивания дерева и в Челябинске и в Перми, поэтому их исключаем из рассмотрения. К сожалению, в этих пунктахпроводилось взвешивание различных тел, но эта разница не влияет на получение качественных результатов и их сравнение. Эти города находятся по разные стороны Уральского хребта и, похоже, по этой причине процесс изменения веса в них отличается от того, который наблюдался в Москве. В Таблица 15.(Челябинск)
таблицах 10-11 показана максимальная разница ∆ Р в весе тел, приведенным к 100 г., за год. Графики 9-10 демонстрируют динамику этого изменения. Сравним качественно графики изменения веса тел в Перми (график 8) и в Челябинске (график 9). Рассмотрим челябинский график изменения веса с 01.10.08
Результаты завешивания изменения тел во времени, полученные в Перми. В Перми с 01.10.08 г. и по 01.11.09 г. завешивались также четыре тела. Это дерево, камень, железо, пластик. Параметры тел отображены в таблице 16, а динамика изменения веса на графике 10.
Таблица 16 (Пермь)
Конечно, делать какие-то выводы из этого графика преждевременно, но тенденция пока прослеживается. В таблице 17 отображены изменения веса тел (приведенные к 100 гр.) в Москве за девять месяца: Не менее существенно и то, что характер изменения московской (график11) и челябинской (график 9) диаграмм металлов несколько коррелируют между собой, и хуже с пермской диаграммой (график 10). И, тем не менее, еще раз подчеркну, на Таблица 17
качественном уровне, эти графики также свидетельствуют об изменение веса тел во времени, подтверждающие самопульсацию Земли с годовым периодом. При исследовании изменения веса тел во времени в МГУ было обнаружено воздействие некоторых тел (слюда, опал) на тарелочку весов до того, как на нее было положено тело. Эффект проявился в 4-м, 3-м и даже 2-м знаке после запятой и при внесении некоторых других тел во внутреннее пространство над чашечкой на высоте 0, 5-2 см (без касания весовой площадки). Это было необычно и свидетельствовало о том, что к чашечке весов подносятся как бы наэлектризованные предметы, а чашечка заряжена одноименно с ними. Дальнейшие исследования показали, что эффект действительно вызывается наличием статического заряда на поверхности тел подносимых к чашечке но не на самой чашечке. На чашечке одноименный заряд обнаружен не был, хотя эффект отталкивания доходил до 4-х граммов. Эта необычная ситуация будет рассмотрена в разделе «Квантование Солнечной системы».
4.2. Изменение орбитальных параметров Земли
Рассмотрим, ориентируясь на таблицы эфемерид, некоторые аспекты годового орбитального движения планеты. Сначала выпишем из справочника [57] величины экстремальных параметров, движения планеты по орбите: • средний радиусы орбиты Rср = 1, 496∙ 1013 cм, • наибольший (афелий) Rасп = 1, 52083∙ 1013 см, и наименьший (перигелий) Rpсп = 1, 47117∙ 1013 см радиус, • большая ось орбиты Rб = 2, 992·1013 см. • средняя скорость движения по орбите vср = 2, 979∙ 106 см∕ сек., − наибольшая (перигелий) vp = 3, 029∙ 106 см∕ сек и наименьшая скорость (афелий) va = 2, 929∙ 106 см∕ сек, и воспользуемся уже упомянутым инвариантом классической механики, найденным еще И. Ньютоном: Rv2 = А = const. (4.4) Уравнение (4.4) используется для нахождения скорости движения тела по орбите на любом расстоянии от Солнца. Его же можно применять и в том случае, когда нужно определить расстояние до спутника или планеты при известной скорости их движения. Интересно, но такая постановка задачи нам нигде не встречалась. Когда началось изучение движения планет с использованием закона всемирного тяготения, законов Кеплера и инвариантов: Rv2 = GMс = R2g = А = const, (4.5) где G постулировалась «единой» для всех тел гравитационная «постоянная», Mс – масса Солнца (4.5): Rava2 = Rpvp2 = const = А, (4.6) где Rа – радиус орбиты в афелии, Rр – радиус в перигелии, то выяснилось, что инвариант (4.6)не выполняется для эллиптической орбиты Земли, и это невыполнение связано с численной величиной радиуса орбиты в афелии и перигелии. Расчетный радиус в экстремальных точках орбиты не совпадал с эмпирически наблюдаемым положением неподвижных звезд и потому не имел объяснения. Найдем, для примера, расчетные величины радиусов орбиты планеты в перигелии и афелии: По инварианту (4.4) определим, чему равняются перигелий и афелий Земли, и сравним их со справочнымиданными. Для этого воспользуемся двумя параметрами Солнца: радиусом – Rс = 6, 96·1010 см, и напряженностью гравитационного поля (ускорением силы тяжести) − gс = 2, 738·104 см⁄ сек2. Сначала определим количественную величину инварианта А, который, как инвариант, остается неизменным для любой точки орбиты: А = Rс2gс = (6, 96·1010)2·2, 738·104 = 1, 32633∙ 1026 см3∕ сек2. Теперь преобразуем (55) относительно v и по известной скорости в афелии vа = 2, 97∙ 106 см∕ сек и перигелии vр = 3, 027∙ 106 см∕ сек определим для планеты расстояния Rа и Rр: Rр = А ∕ vр2 = 1, 4475∙ 1013 см. Rа = А ∕ vа2 = 1, 5036∙ 1013 см. Оба расстояния не совпадают с данными из астрономического справочника [57]: Rа ≠ Rасп и Rр ≠ Rсп. Да и большая ось орбиты, по расчету равная 2, 951∙ 1013 см, на 4, 1 млн. км меньше представленной в справочнике 2, 992∙ 1013 см. Чем обусловлено несовпадение было не ясно, но понятно, что именно оно накладывает табу на применение совершенно корректного инварианта (4.4) для расчета радиусов орбиты по известной скорости движения планеты. Ни теоретического, ни эмпирического объяснение этому несовпадению найдено не было. И тогда астрономы стали подгонять под явление сложное математическое обоснование, включающее неизменные массы планеты и светила. Целью подгонки было совмещение фиксируемого изменения орбитальной скорости движения планеты с изменением радиуса орбиты таким образом, чтобы не нарушался принцип инерционного движения. Т.е. было постулировано, что планета, движется по орбите неправильно, ежемесячно замедляясь и ускоряясь. Исходя из того, что орбита Земли не круговая, а эллиптическая ученые предположили (постулировали), что уравнение (4.4) для эллиптической орбиты инвариантом не является: Rv2 ≠ const, и выполняется только для круговой орбиты, а для эллиптической вывели из решения задачи Кеплера «... два инварианта (интегралы движения): энергии и момента импульса:
где Проведя далее целый ряд математических преобразований, не имеющих физического смысла и не связанных с условиями движения планеты, в конечном итоге нашли уравнения параметров радиуса через параметры орбиты – её большую полуось В афелии:
В перигелии:
Постулированиенекорректности инварианта (4.4) для эллиптических орбитразорвало все связи движущейся планеты с вещественным пространством, вычленило ее из структуры Солнечной системы, и превратило в инерциальную систему отсчета, в абстракцию, в мнимость. Поэтому все дальнейшие операции с орбитой, включая нахождение монотонного изменения радиуса орбиты, не имели никакого физического смысла, не говоря уж о том, что траектория орбиты Земли оказывается вычисленной с большой погрешностью (например, как будет показано далее, эксцентриситет орбиты оказался заниженным в два раза). К тому же, хотя радиусы эксцентриситетов вычисляются (4.8)-(4.9) с точностью до четвертого знака, неизбежным следствием такого расчета становится диспропорциональность экстремумов скорости и радиуса в местах наибольшего и наименьшего удаления планеты от светила. И эта диспропорциональность проявляется и в перигелии, и в афелии как несовпадении экстремумов скорости движения и радиусов орбит, причем достаточно значительного: от нескольких дней до двух недель, т.е. с точностью до третьего и даже второго знака, что для астрономии, считающейся очень точной наукой, вряд ли допустимо. Чтобы разобраться в этом вопросе, проанализируем как монотонно или не монотонно изменяется расстояние и скорость движения Земли по орбите, опираясь на ту же систему эфемерид (приложение 1, v и R). При этом имеем в виду, что взаимосвязь скорости и расстояния как для круговой так и для эллиптической орбиты (4.4) предполагает одинаковый монотонный или не монотонный характер изменения обоих параметров, а нелинейность инварианта (4.4) свидетельствует о волновом изменении этих параметров. Для примера можно выбрать любой отрезок времени: годовой или месячный. Я выбрал отрезок с 20 июня по 25 июля 2005 года потому, что именно в это время орбитальная скорость v планеты оказывается минимальной, а расстояние до светила R максимальным.И эти экстремумы должны, согласно классической механике, приходиться на один временной отрезок (на одну дату). Переносим из таблиц эфемерид параметры скорости v на график 12, и получаем, что скорость планеты в движении по орбите, даже на протяжении одного месяца, меняется по волновому закону. Её скорость то возрастает, то замедляется. Но если планета в своем движении то разгоняется, то притормаживает, она движется не по инерции, а взаимодействуя с чем-то непроявленным. Т.е. фактически нарушает I-й закон классической механики – закон инерции. Это очень удивительное явление. Оно свидетельствует о том, что планета летит в космическом пространстве не по инерции, а взаимодействуя с окружающим телесным пространством (с
График 12. График 13. эфиром). А поскольку скорость v орбиталь-ного движения планеты связана инвариантом (4.4) с параметром ее орбитального радиуса R, то надо ожидать, что радиус орбиты тоже изменяется по волновому закону. Проверим соблюдение этой закономерности, построив диаграмму ежедневного изменения радиуса орбиты R1за тот же временной интервал (график 13). Никакого волнообразного изменения расстояния между Солнцем и планетой на этом графике не отмечается. Расстояние между ними в июле месяце продолжает монотонно возрастать, а затем с июля до января 2006 г. так же монотонно убывать, что как бы свидетельствуе
|

 На графике 5 показаны ежедневные диаграммы измене-ния веса всех тел за год, при-веденные к 100 гр. весу (кроме дубового бруска). Вес дубового бруска меняется на несколько грамм, и это изменение корре-лирует с временами года. Отсчет времени ведется с 01.07.05 г. по График 5. 01.07.06 г.
На графике 5 показаны ежедневные диаграммы измене-ния веса всех тел за год, при-веденные к 100 гр. весу (кроме дубового бруска). Вес дубового бруска меняется на несколько грамм, и это изменение корре-лирует с временами года. Отсчет времени ведется с 01.07.05 г. по График 5. 01.07.06 г.
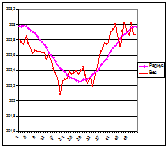
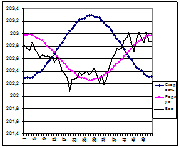 График 8 свидетельствует – расчетное изменение радиуса ор-биты (диаграмма «радиус») про-порционально изменению орби-тальной скорости (диаграмма «скорость»). Диаграмма «вес» — изменения веса свинца с неко-торым отставанием «копирует» изменение орбиты планеты, уменьшаясь к перигелию, где График 8. напряженность гравиполяСолнеч-ной системынаибольшая и возрастая к афелию — где онанаименьшая. Таким образом, график отображает то обстоятельство, что изменение веса тел на поверхности Земли обусловлено прохождением планеты по областям изменяющейся напряженности гравиполя Солнечной системы.
График 8 свидетельствует – расчетное изменение радиуса ор-биты (диаграмма «радиус») про-порционально изменению орби-тальной скорости (диаграмма «скорость»). Диаграмма «вес» — изменения веса свинца с неко-торым отставанием «копирует» изменение орбиты планеты, уменьшаясь к перигелию, где График 8. напряженность гравиполяСолнеч-ной системынаибольшая и возрастая к афелию — где онанаименьшая. Таким образом, график отображает то обстоятельство, что изменение веса тел на поверхности Земли обусловлено прохождением планеты по областям изменяющейся напряженности гравиполя Солнечной системы. по 01.11.09. По всем телам фиксируется изменение веса в четвертом знаке, а по дереву – в третьем. Из неорганических тел наи-большее изменение веса зафиксировано у Оргстек- График 9. ла (см. табл. 11). Это достаточно значительные изменение, такие же по величине, как и те, что фиксируется при определении гравитационной «постоянной» и можно полагать, что они имеют одинаковую природу.
по 01.11.09. По всем телам фиксируется изменение веса в четвертом знаке, а по дереву – в третьем. Из неорганических тел наи-большее изменение веса зафиксировано у Оргстек- График 9. ла (см. табл. 11). Это достаточно значительные изменение, такие же по величине, как и те, что фиксируется при определении гравитационной «постоянной» и можно полагать, что они имеют одинаковую природу. Сопоставление таблиц показывает, что изменение веса ∆ Р металла с западной стороны Урала и твердых тел с его восточной стороны от-личаются значительно. Конечно, эти материа-лы имеют разные свой-ства, но вряд ли эту разницу можно отнес-ти на свойства. Не График 10. исключено влияние и каменного основания Урала. Но однпорядковые величины изменений веса металлов просматриваются и в результатах взвешиваний в Москве 2005-06 гг. В сентябре 2009 г. в Москве ученые (Рукин М., Жарвин Н. МГУ, при участии автора) решили экспериментально проверить изменение веса девяти тел при длительным их взвешиванию.
Сопоставление таблиц показывает, что изменение веса ∆ Р металла с западной стороны Урала и твердых тел с его восточной стороны от-личаются значительно. Конечно, эти материа-лы имеют разные свой-ства, но вряд ли эту разницу можно отнес-ти на свойства. Не График 10. исключено влияние и каменного основания Урала. Но однпорядковые величины изменений веса металлов просматриваются и в результатах взвешиваний в Москве 2005-06 гг. В сентябре 2009 г. в Москве ученые (Рукин М., Жарвин Н. МГУ, при участии автора) решили экспериментально проверить изменение веса девяти тел при длительным их взвешиванию.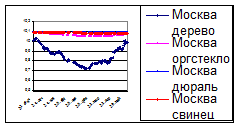 Для проведения экспери-ментов использовались электронные весы закры-того типа, KEPN 770/GS/Gc/, версии 2.3 04/2000 г., точность измерения (в граммах) – пятый знак после запя- График 11. той. И хотя прошло всего девять месяцев, первые результаты зафиксировали эти изменения. На графике 11 отображены те же тела, приведенные к весу ~10 гр., которые взвешиваются в Челябинске, и видно, что все они, (кроме дерева), в течение всего времени наблюдения медленно (медленнее других – дюраль) уменьшают свой вес.
Для проведения экспери-ментов использовались электронные весы закры-того типа, KEPN 770/GS/Gc/, версии 2.3 04/2000 г., точность измерения (в граммах) – пятый знак после запя- График 11. той. И хотя прошло всего девять месяцев, первые результаты зафиксировали эти изменения. На графике 11 отображены те же тела, приведенные к весу ~10 гр., которые взвешиваются в Челябинске, и видно, что все они, (кроме дерева), в течение всего времени наблюдения медленно (медленнее других – дюраль) уменьшают свой вес.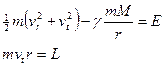 (4.7)
(4.7) - гравитационная «постоянная», М – масса Солнца, m – масса Земли,
- гравитационная «постоянная», М – масса Солнца, m – масса Земли,  и
и  - радиальная и тангенциальная компоненты скорости. В афелии и перигелии
- радиальная и тангенциальная компоненты скорости. В афелии и перигелии  ».
».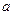 и эксцентриситет
и эксцентриситет  орбиты в афелии, и перигелии в следующем виде, позволяющем более или менее точно совместить изменение орбитальной скорости и радиуса:
орбиты в афелии, и перигелии в следующем виде, позволяющем более или менее точно совместить изменение орбитальной скорости и радиуса: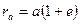 ,
,  . (4.8)
. (4.8) ,
,  . (4.9)
. (4.9)