И вывод расчетной формулы. Существует несколько методов определения модуля упругости
Существует несколько методов определения модуля упругости. В данной работе используется метод, основанный на деформации изгиба. Установка для определения модуля упругости (рис. 4.3) состоит из подставки, на которой расположены вертикальные стойки 1 с опорными призмами. На призмы помещается испытуемый образец 2. К середине стержня при помощи специального устройства 3 навешиваются грузы, которые деформируют (изгибают) стержень. Величину деформации (стрелу прогиба) измеряют с помощью индикатора 4.
Рис. 4.3.
Для определения модуля упругости по деформации изгиба необходимо знать величину деформирующей силы, приложенной к середине стержня и вызывающей его изгиб F, и стрелу прогиба l, т. е. величину смещения средней части стержня от первоначального положения (рис. 4.4). Теоретические расчеты показывают, что для стержня любого сечения стрела прогиба определяется по формуле
Отсюда
где Е – модуль упругости (Юнга);
изгиба;
Q – коэффициент, характеризующий форму стержня.
Рис. 4.4.
Для стержня прямоугольного сечения шириной а и толщиной b (рис. 4.5, а)
Для квадратного сечения
В случае сплошного стержня (рис. 4.5, б)
Для трубки с наружным радиусом
Рис. 4.5. Подставляя эти значения в формулу (4.6), получим выражение для определения модуля упругости. Для стержней прямоугольного сечения
квадратного сечения
трубки
сплошного стержня кругового сечения
|
. (4.5)
, (4.6)
– сила, действующая на стержень и вызывающая деформацию
– длина стержня;
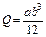. (4.7)
. (4.8)
. (4.9)
и внутренним 
(рис. 4.5, в)
. (4.10)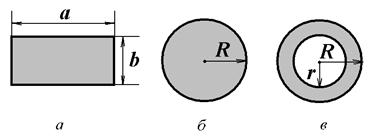
, (4.11)
, (4.12)
, (4.13)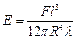
. (4.14)
